| Главная » Статьи » Физика и математика » Мои статьи |
Кориолисово ускорение
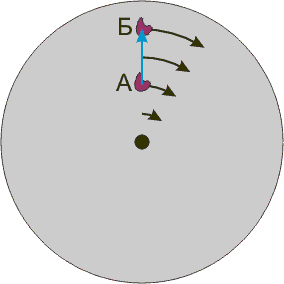
При вращении диска, более далёкие от центра точки движутся с большей касательной скоростью, чем менее далёкие (группа чёрных стрелок вдоль радиуса). Если мы хотим переместить некоторое тело вдоль радиуса, так, чтобы оно оставалось на радиусе (синяя стрелка из положения «А» в положение «Б»), то нам придётся увеличить скорость тела, то есть, придать ему ускорение. Если наша система отсчёта вращается вместе с диском, то мы ощутим, что тело «не хочет» оставаться на радиусе, а «норовит» уйти влево — это и есть сила Кориолиса.
 Движение шарика по поверхности вращающейся тарелки.
Си́ла Кориоли́са (по имени французского учёного Гюстава Гаспара Кориолиса, впервые его описавшего) — одна из сил инерции, существующая в неинерциальной (вращающейся) системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения. Ускорение Кориолиса было получено Кориолисом в 1833 г., Гауссом в 1803 г. и Эйлером в 1765 г. Причина появления силы Кориолиса — в кориолисовом (поворотном) ускорении. Для того, чтобы тело двигалось с кориолисовым ускорением, необходимо приложение силы к телу, равной F = ma, где a — кориолисово ускорение. Соответственно, тело действует по третьему закону Ньютона с силой противоположной направленности. FK = − ma. Сила, которая действует со стороны тела, и будет называться силой Кориолиса. Не следует путать Кориолисову силу с другой силой инерции — центробежной силой, которая направлена по радиусу вращающейся окружности. В инерциальных системах отсчёта действует закон инерции, то есть, каждое тело стремится двигаться по прямой и с постоянной скоростью. Если рассмотреть движение тела, равномерное вдоль некоторого вращающегося радиуса и направленное от центра, то станет ясно, что чтобы оно осуществилось, требуется придавать телу ускорение, так как чем дальше от центра, тем должна быть больше касательная скорость вращения. Это значит, что с точки зрения вращающейся системы отсчёта, некая сила будет пытаться сместить тело с радиуса. Если вращение происходит по часовой стрелке, то двигающееся от центра вращения тело будет стремиться сойти с радиуса влево. Если вращение происходит против часовой стрелки — то вправо.
Математическое определение Сила Кориолиса равна: где m — точечная масса, Кориолисово ускорение — это векторная величина, равная ПолучениеПусть тело совершает сложное движение: движется относительно неинерциальной системы отсчёта со скоростью Тогда линейная скорость тела в инерциальной системе координат равна:
где
Найдём значение каждого слагаемого в инерциальной системе координат:
Таким образом, получаем:
Физический смыслПусть тело движется со скоростью
Тогда данное движение приведёт к изменению расстояния до центра вращения R и, как следствие, абсолютной скорости движения точки неинерциальной системы отсчёта, совпадающей с движущейся точкой. Как мы знаем, эта скорость движения равна Данное изменение будет равно:
Проведя дифференцирование по времени, получим C другой стороны, вектор
Общее ускорение будет Если тело движется перпендикулярно направлению к центру вращения, то доказательство будет аналогичным. Ускорение из-за поворота вектора скорости останется *** Энциклопедия «Элементы большой науки», «Природа Науки» Эффект Кориолиса. Представьте, что кто-то, находясь на Северном полюсе, бросил мяч кому-то, кто находится на экваторе. Пока мяч летел, Земля немного повернулась вокруг своей оси, и ловящий успел сместиться к востоку. Если бросающий, целясь мячом, не учел этого движения Земли, мяч упал западнее (или левее) ловящего. С точки зрения человека на экваторе получается, что мяч летел левее, чем надо, с самого начала — как только его выпустил из рук бросающий, — и до тех пор, пока не приземлился. Согласно законам механики Ньютона, чтобы движущееся прямолинейно тело отклонилось от изначально заданной траектории, на него должна действовать какая-то внешняя сила. Значит, ловящий на экваторе должен сделать вывод, что брошенный мяч отклонился от прямолинейной траектории под действием некоей силы. Если бы мы смогли посмотреть на летящий мяч из космоса, мы бы увидели, что на самом деле никакая сила на мяч не действовала. Отклонение же траектории было вызвано тем, что Земля успела повернуться под мячом, пока он летел по прямой. Таким образом, действует в подобной ситуации какая-то сила или нет, — это целиком зависит от системы отсчета, в которой находится наблюдатель. И подобное явление неизбежно возникает, когда есть какая-нибудь вращающаяся система координат — например, Земля. Для описания этого явления физики часто используют выражение фиктивная сила, имея в виду, что сила «реально» отсутствует, просто наблюдателю во вращающейся системе отсчета кажется, что она действует (другой пример фиктивной силы — это центробежная сила). И противоречий здесь нет никаких, поскольку оба наблюдателя единодушны относительно реальной траектории полета мяча и уравнений, ее описывающих. Расходятся они лишь в терминах, которые они используют для описания этого движение. Нетрудно понять, что в Северном и Южном полушариях сила Кориолиса действует на движущееся тело в прямо противоположных направлениях. Именно поэтому в Северном полушарии вихри циклонов кажутся закрученными против часовой стрелки, а в Южном — по часовой стрелке. Отсюда происходит бытующее в народе убеждение, что вода в канализационных отверстиях ванн и раковин в двух полушариях вращается в противоположных направлениях, — якобы это обусловлено эффектом Кориолиса. На самом же деле, хотя и верно, что сила Кориолиса действует противоположно в двух полушариях, направление закручивания воды в сливной воронке лишь отчасти определяется этим эффектом. Дело в том, что вода долгое время течет по водопроводным трубам, при этом в потоке воды образуются течения, которые, хоть их и трудно увидеть простым глазом, продолжают закручивать струю воды и тогда, когда она льется в раковину. Кроме того, когда вода уходит в сливное отверстие, могут создаваться похожие течения. Именно они определяют направление движения воды в воронке, поскольку силы Кориолиса оказываются гораздо слабее этих течений. В обычной жизни направление закручивания воды в сливной воронке в северном и южном полушариях больше зависит от конфигурации канализационной системы, чем от действия природных сил. Однако все-таки нашлась группа экспериментаторов, которой хватило терпения повторить этот опыт в «чистых» условиях. Они взяли идеально симметричную раковину сферической формы, устранили канализационные трубы, позволив воде проходить сквозь сливное отверстие свободно, оборудовали сливное отверстие автоматической заслонкой, которая открывалась лишь после того, как в воде успокаивались любые остаточные токи, — и увидели-таки эффект Кориолиса в действии! Несколько раз им даже удалось увидеть, как вода сначала под слабым внешним воздействием закручивалась в одну сторону, а затем силы Кориолиса брали верх, и направление спирали менялось на противоположное! *** Этот материал попал в категорию "Мои статьи", т.к. он предполагает наши возражения официальной теории явления Кориолиса, которые изложены в следующих статьях: 2. Отклонение от вертикали свободно падающих тел в условиях Земли 3. Эта странная сила Кориолиса 4. Определение силы и ускорения Кориолиса при помощи мерной динамики вращательного движения 5. Ошибки Фейнмана при выводе формулы Кориолиса 6. Три абсурда теоремы Кориолиса 7. Центростремительное ускорение беременно ускорением Кориолиса?Ё!!! Да, неужели!Ё! 9. Куда и почему вращается вода в воронках и воздушные вихри в атмосфере
| ||
| Просмотров: 2119 | | ||
| Всего комментариев: 0 | |
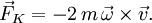
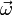 —
— 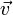 — вектор скорости движения точечной массы.
— вектор скорости движения точечной массы.![\vec{a}_k=2 \left[ \vec \omega \times \vec v \right],](http://dic.academic.ru/pictures/wiki/files/55/7b078ba4ad487c59c24ab9381f405b3f.png) где
где 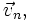 а сама система движется поступательно с линейной скоростью
а сама система движется поступательно с линейной скоростью 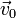 в инерциальной системе координат и одновременно вращается с угловой скоростью
в инерциальной системе координат и одновременно вращается с угловой скоростью 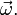
![\vec v= \vec {v}_0 + \left[ \vec \omega \times \vec R \right] + \vec {v}_n,](http://dic.academic.ru/pictures/wiki/files/100/d3ee4158828c2b1125e1761fd6670ab5.png)
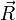 — радиус-вектор центра масс тела относительно неинерциальной системы отсчета. Продифференцируем данное уравнение:
— радиус-вектор центра масс тела относительно неинерциальной системы отсчета. Продифференцируем данное уравнение:![\frac{d}{dt}\vec v= \frac{d}{dt}\vec {v}_0 + \frac{d}{dt}\left[ \vec \omega \times \vec R \right] +\frac{d}{dt} \vec {v}_n.](http://dic.academic.ru/pictures/wiki/files/51/3af4b9a812a8b372387d54168f2dba94.png)
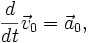
![\frac{d}{dt} \vec {v}_n = \vec {a}_n + \left[ \vec\omega \times \vec {v}_n \right],](http://dic.academic.ru/pictures/wiki/files/53/564bf2b000132c2b979c4abe8bbcd2c5.png)
![\frac{d}{dt} \left[ \vec\omega \times \vec R \right] = \left[ \vec \varepsilon \times \vec R \right] + \left[ \vec\omega \times \frac{d}{dt} \vec R \right] = \left[ \vec \varepsilon \times \vec R \right] + \left[ \vec\omega \times \vec {v}_n \right] + \left[ \vec\omega \times \left[ \vec\omega \times \vec R \right] \right],](http://dic.academic.ru/pictures/wiki/files/101/e5ef1554861e7cb48ef0e7a990349ddd.png) где
где 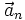 — линейное ускорение относительно системы,
— линейное ускорение относительно системы, 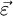 — угловое ускорение.
— угловое ускорение.![\frac{d}{dt}\vec v = \vec a=\vec {a}_0 + \vec {a}_n + \left[ \vec \varepsilon \times \vec R \right] + \left[ \vec \omega \times \left[ \vec \omega \times \vec R \right] \right] + 2\left[ \vec \omega \times \vec {v}_n \right].](http://dic.academic.ru/pictures/wiki/files/99/cee134148f3010b2696e9e0f94b9b9d3.png) Последнее слагаемое и будет кориолисовым ускорением.
Последнее слагаемое и будет кориолисовым ускорением.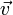 вдоль прямой к центру вращения инерциальной системы отсчёта.
вдоль прямой к центру вращения инерциальной системы отсчёта.![\vec {v}_e = \left[ \vec \omega \times \vec R \right].](http://dic.academic.ru/pictures/wiki/files/97/aa9de6f46034488f4bbca755d76bc9f5.png)
![d \vec {v}_e= \left[ \vec\omega \times d \vec R \right].](http://dic.academic.ru/pictures/wiki/files/48/0baa1c9caf22087ed731e63f30de4be5.png)
![\vec a = \left[ \vec\omega \times \vec v \right]](http://dic.academic.ru/pictures/wiki/files/99/c8317f0075818272e2bc3cd7e7b8b78d.png) (направление данного ускорения перпендикулярно
(направление данного ускорения перпендикулярно 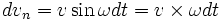 при
при 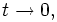 соответственно второе ускорение будет:
соответственно второе ускорение будет:![\vec {a}_k=2 \left[ \vec\omega \times \vec v \right].](http://dic.academic.ru/pictures/wiki/files/50/2852b6463402e829d89a249960f33f2c.png) Как видно, система отсчёта не претерпела изменения угловой скорости
Как видно, система отсчёта не претерпела изменения угловой скорости 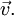 Тем не менее, ускорение не равно нулю.
Тем не менее, ускорение не равно нулю.![\vec a = \left[ \vec\omega \times \vec v \right],](http://dic.academic.ru/pictures/wiki/files/51/3537afd827222e73c0737864244d6b7b.png) а также прибавляется ускорение в результате изменения центростремительного ускорения точки.
а также прибавляется ускорение в результате изменения центростремительного ускорения точки.