| Главная » Статьи » Физика и математика » Мои статьи |
СИЛЫ КОРИОЛИСА В ГИРОСКОПЕ. В описании механизма прецессии мы будем пользоваться понятиями классической динамики вращательного движения знакомой и привычной для людей, увлекающихся физикой. Здесь и далее мы будем отдельно оговаривать только те случаи, в которых понятия классической динамики вращательного движения принципиально не соответствуют общему физическому смыслу явлений и истинной динамике вращения. Гироскопом называется быстровращающееся симметричное твердое тело, ось вращения которого может изменять свое направление в пространстве. Рассмотрим, как образуется прецессия. Рисунки заимствованы из статьи «Почему и как прецессирует гироскоп», размещённой на сайте кафедры ОиСФ МИФИ под названием «В помощь студентам, изучающим физику» (http://iatephysics.narod.ru/gyroscope/gyrosc_r.htm).
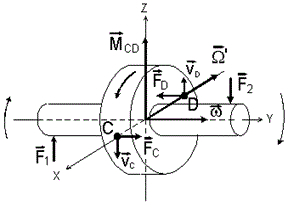
Рис. 4.7.1
Пусть к оси (у) гироскопа постоянно приложены постоянные силы (F1) и (F2), создающие момент (M12), перпендикулярный к плоскости, в которой лежат силы (см. Рис. 4.7.1). Под действием момента (M12) гироскоп начинает поворачиваться относительно оси (х) с какой-то угловой скоростью (Ω'). При этом точки (С) и (D) с массами (dm) оказываются движущимися в радиальном направлении вращательного движения относительно оси (х). Следовательно, на них, как пишет автор статьи, начинают действовать силы Кориолиса (FС = dm [VС, Ω']) и (-FD = dm [VD, Ω']), которые и вызывают прецессию гироскопа, т.е. его вращение относительно оси (z) с угловой скоростью (Ω). Здесь повторяются те же самые ошибки, что и у Фейнмана, у которого фиктивная сила Кориолиса «толкает его (тело – ААА) в бок» (см. гл. 4.2.). Но силы Кориолиса не могут ничего и никого толкать в бок или куда-либо ещё. Это фиктивные, т.е. несуществующие силы инерции. Следовательно силы Кориолиса никак не могут вызывать прецессию гироскопа. Очень странно, что эта ошибка повторяется практически на регулярной основе у многих авторов, в том числе и довольно именитых. Не свидетельствует ли это о том, что природа явления Кориолиса до сих пор так и не раскрыта официальной физикой? В классической физике нет истинных сил Кориолиса-Кеплера или просто сил Кеплера. Однако это единственная реальная сила, которая действует в направлении фиктивных сил инерции Кориолиса. Следовательно, это единственная сила, которая может запустить прецессию гироскопа и успешно противостоять внешним силам (F1) и (F2). Поэтому в дальнейшем под силами (FC) и (FD) будем понимать силы Кориолиса-Кеплера. Итак, прецессия происходит следующим образом (см. Рис. 4.7.2).
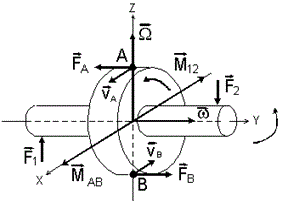
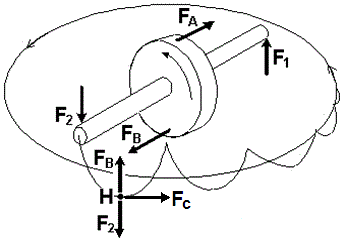
Рис.4.7.2 Вращение относительно оси (z) является в свою очередь переносным вращением для точек (А) и (В). Следовательно, на них действуют силы Кориолиса (-FА = dm [VА, Ω]) и (FВ = dm [VВ, Ω']), которые образуют момент (MAB), стремящийся уравновесить внешний момент (M12). С увеличением скорости прецессии под действием постоянного момента (M12) растёт и момент (MAB), в то время как противодействующий ему момент постоянных внешних сил (M12), запускающий прецессию, остаётся неизменным. Следовательно, в какой-то нижней точке траектории прецессии (Н) момент (MAB) сначала сравняется с моментом (M12) по величине, а затем и неминуемо превысит его (см. Рис. 4.7.3).
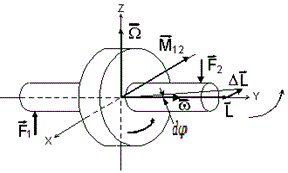
Рис. 4.7.4 Под действием силы (FB) и (FA) момента (MAB) ось (y) начинает двигаться из нижней точки (Н) вверх по рисунку, что приводит к изменению знака угловой скорости вращения гироскопа (Ω') относительно оси (х). При этом направление сил Кориолиса-Кеплера (FC) и (FD) и соответственно момента (MCD) так же изменяется на противоположное. В результате под действием обратных сил (FC) и (FD) скорость прецессии уменьшается, т.е. момент (MCD) теперь тормозит прецессию. Когда скорость прецессии окажется меньше необходимой, чтобы компенсировать момент пары сил (F1) и (F2), знак (Ω') снова изменится, и процесс начнет повторяться. Такое колебательное движение гироскопа вокруг оси x называется нутацией (см. Рис. 4.7.4). Классическая теория утверждает, что из-за трения нутация прекращается и гироскоп переходит в режим установившейся прецессии, при котором |MAB| = | M12|. Однако нутация - это и есть проявление механизма формирования прецессии, в котором за счёт отрицательной обратной связи происходит регулирование равновесного в целом противодействия сил Кеплера с внешними силами (F1) и (F2). Без движения оси Х под действием сил (F1) и (F2), с которого и начинаются нутации и прецессия нет и не может быть явления Кориолиса. Поэтому нутации прекращаются только с прекращением самой прецессии. А трение способствует прекращению нутации ровно в той степени, в которой оно способствует прекращению всех движений в принципе. Как известно, регулирующее воздействие принципиально запаздывает по отношению к регулируемым параметрам, т.к. оно является ответным на регулируемое воздействие. Сначала появляется отклонение параметра и только после этого вырабатывается ответное регулирующее воздействие, что неизбежно связано с погрешностью регулирования, которая, таким образом, является следствием запаздывания регулирующего воздействия. Нутации это и есть следствие неустранимой погрешности регулирования механизма прецессии. Равенство (|MAB| = |M12|) в установившейся прецессии является лишь примерным равенством (|MAB| ≈ |M12|), погрешность которого и определяют нутации. С ростом частоты нутаций уменьшается время запаздывания регулирования и соответственно повышается его точность. Однако поскольку запаздывание регулирования принципиально неустранимо, то принципиально неустранима и его погрешность и соответственно нутации. Автоматическое регулирование и соответственно нутации присутствует на микроуровне даже в равномерном вращательном движении. Это циклы его формирования, которые в переходном процессе образования вращения, точно так же, как и в начале прецессии гироскопа имеют большую амплитуду и малую частоту. В установившейся регулярной прецессии точно так же, как и в установившемся вращении эти колебания никуда не исчезают (см. гл. 3.2.). Они лишь переходят на микроуровень. Классическая физика утверждает, что прецессия осуществляется за счёт работы внешних сил, причём только на начальном этапе её запуска. При этом энергетика основного вращения гироскопа во время прецессии якобы не изменяется, а в нутациях осуществляется только преобразование потенциальной энергии внешней силы в кинетическую энергию прецессии гироскопа и обратно. После наступления регулярной прецессии, нутации якобы полностью прекращаются, а внешняя сила только поддерживает прецессию по аналогии с центростремительной силой равномерного вращательного движения. (см. Д. В. Сивухин, Общий курс физики, Механика, Т1, М., 1979 г., 520 с., глава 7, параграф 50, стр. 274). Можно, конечно не знать физического механизма формирования равномерного вращательного движения, проявляющегося в виде автоколебаний его параметров на микроуровне. Можно считать эти колебания побочным явлением так же, как и нутации в прецессии гироскопа, как утверждает классическая физика. Однако при этом энергетическая независимость равномерного вращательного движения с его внутренней центростремительной силой, хотя бы не противоречит закону сохранения энергии замкнутой системы. А вот равномерная без затратная прецессия под воздействием внешней силы - это прямое нарушение закона сохранения энергии, который принципиально не может соблюдаться при наличии внешних сил. Верно и обратное утверждение. Внешние силы, которые не совершают работы над системой, не могут быть внешними для системы силами. Такие силы являются внутренними силами системы. Однако силы (F1) и (F2) вряд ли можно назвать внутренними силами системы гироскопа. Это внешние силы, которым противостоит сила Кеплера со стороны элементов диска гироскопа (dm). При этом элементы (dm) замедляются и теряют свою энергию. Совершенно очевидно, что силы Кеплера, отвечающие за прецессию питаются энергией быстрого вращения гироскопа. Это легко проверить на электрическом управляемом гироскопе через изменение быстрого вращения диска гироскопа. При увеличении скорости вращения диска траектория прецессии поднимется выше, а при падении оборотов, со временем, она опустится. Но если мячик вдруг прыгнул «выше головы», то запасами его потенциальной энергии перед падением этого уже не объяснить. Как следует из приведённого описания, прецессия запускается с нуля в начале цикла нутации и полностью останавливается в конце цикла. Следовательно, в каждой нутации на разгон и торможение прецессии неизбежно затрачивается энергия. При этом существует не абсолютно неизменная постоянная скорость прецессии, как утверждает классическая физика, а только её постоянная средняя скорость. Таким образом, прецессия — это старт-стопное движение, на разгон и торможение которого затрачивается энергия быстрого вращения гироскопа. При этом постоянная скорость регулярной прецессии - есть средняя скорость старт-стопной прецессии. Теперь, имея некоторые качественные представления о классической теории гироскопа и её противоречиях, перейдём к рассмотрению динамики прецессирующего гироскопа количественно. Начнём с классической динамики гироскопа, приведённой в работе А.Н. Матвеева, Механика и теория относительности, Глава 11 Динамика твёрдого тела, стр. 325, 326, М.: Высшая школа, 1986 (см. курсив): В результате прецессии полная скорость прецессии (ω + Ω) не совпадает с осью гироскопа (см. Рис. 4.7.6). Однако в виду того, что (ω>> Ω) это несовпадение незначительно и поэтому, несмотря на наличие прецессии, угловая скорость быстрого вращения гироскопа практически совпадает с его осью симметрии и с моментом импульса (L). Тогда угловая скорость прецессии легко может быть вычислена из уравнения моментов. dL / dt = M12 Отсюда: dL = M12 * dt, но приращения момента импульса (L) можно определить через момент импульса и приращение угла его поворота в прецессионном вращении (см. Рис. 4.7.6):
Рис. 4.7.4 Из рисунка видно, что: dL = L * dφ, т.е. dL = M12 * dt = L * dφ Отсюда угловая скорость прецессии равна: Ω = dφ / dt = M12 / L = M12 / (I * ω) Как это ни странно, в классическом выводе скорости прецессии начисто отсутствуют силы Кеплера, которые наряду с внешними силами запускают прецессию и являются неотъемлемой частью её механизма. Из приведённого выше описания механизма прецессии следует, что энергетически прецессия питается энергией внешней силы и энергией основного вращения, проявляющихся в одном взаимодействии. А поскольку сила взаимодействия для взаимодействующих тел является общей, то за истинную силу Кориолиса-Кеплера правомерно принять, как внешнюю силу, так и равную ей силу элементов (dm), т.е. собственно саму истинную силу Кориолиса-Кеплера. Обозначив запускающий прецессию момент сил Кеплера индексом (к), прецессию индексом (п), а момент импульса гироскопа индексом (г) можно записать: |МК| = dLГ / dt = |MП| = dLП / dt При этом, несмотря на расчёт вращения прецессии по её средним постоянным параметрам, мы фактически определяем только динамику пуска или останова псевдо равномерной старт-стопной прецессии. Для основного вращения гироскопа эта динамика его торможения.
| |
| Просмотров: 4053 | |
| Всего комментариев: 0 | |