| Главная » Статьи » Физика и математика » Мои статьи |
Очевидно, новая энергия связи, необходимая для установления нового вращения, которая аккумулируется в связующем теле, может быть изъята только из энергии прежнего окружного движения (Ек1) в виде отрицательной работы центростремительной (центробежной) силы Ецсс (Ецб) на участке равном разности радиусов (Δr = r2 - r1). При этом отбор необходимой энергии осуществляется через истинную силу Кориолиса-Кеплера, которая является результирующей радиальной силы (Fr) и ньютоновской силы инерции поэлементной поддержки (Fипэп), устанавливающей новую связь путём ограничения радиального движения. Оставшаяся часть - это и есть энергия (Ек2) нового окружного движения с новой линейной скоростью (V2). Математически это можно выразить следующим образом: Ек2 = Ек1 – Ецсс, где Ек1 = m * V12 / 2 Ецб = m * ацс * Δr Определим ЦСС (ЦБС). Начальное и конечное значения силы упругости связующего тела на удлинении (Δr) равно ЦСС для начальной и конечной линейной скоростью (V1) и (V2) соответственно. А поскольку сила упругости изменяется прямо пропорционально удлинению, т.е. линейно, то новая энергия связи, как мы отмечали выше, эквивалентна работе средней ЦСС (Fцссср) со средним центростремительным ускорением, определяющимся средней линейной скоростью и средним радиусом. Fцбср = m * (½ * (V1 + V2)) 2 / ((r2 + r1)/2) = = ¼ * m * (V1 + V2) 2 / ((r2 + r1)/2) = ½ * m * (V1 + V2) 2 / (r2 + r1) Тогда работа средней ЦСС (Fцссср) на участке (Δr = r2 – r1) равна: Ецсс = Fцссср * Δr = m * (½ * (V12 + 2 * V1* V2 + V22) * (r2 – r1)) / (r2 + r1) С учётом значений (Ек1) и (Ецсс) кинетическая энергия нового окружного движения, определяющаяся по формуле для удлиняющегося радиуса (Ек2 = Ек1 – Ецсс, см. выше) равна: Ек2 = m * V22/2 = m * V12/2 – m * (½ * (V12 + 2 * V1* V2 + V22) * (r2 – r1)) / (r2 + r1) Покажем последовательные преобразования полученного выражения для (Ек2), предварительно сократив его на множитель (m): V22/2 = V12/2 – (½ * (V12 + 2 * V1* V2 + V22) * (r2 – r1)) / (r2 + r1); V22 = V12 – (V12 + 2 * V1* V2 + V22) * (r2 – r1)) / (r2 + r1); V22 – V12 = – (V12 + 2 * V1* V2 + V22) * (r2 – r1)) / (r2 + r1); V22 – V12 = – (V12 + 2 * V1* V2 + V22) * (r1 – r2)) / (r2 + r1); V22 * r1 + V22 * r2 – V12 * r1 – V12 * r2 = (V12 + 2 * V1* V2 + V22) * (r1 – r2) V22 * r1 + V22 r2 – V12 * r1 – V12 * r2 = V12 * r1 + 2 * V1* V2 * r1 + + V22 * r1 – V12 * r2 – 2 * V1* V2 * r2 – V22 r2; 2 * V22 r2 – 2 * V12 * r1 – 2 * V1* V2 * r1 + 2 * V1* V2 * r2 = 0; V22 r2 – V12 * r1 – V1* V2 * r1 + V1* V2 * r2 = 0; V22 r2 + (V1* r2 – V1* r1) * V2 – V12 * r1 = 0; Последнее уравнение, полученное после преобразования и сокращения, представляет собой квадратное уравнение вида: А * х2 + В * х – С = 0, где х = V2 Корни этого уравнения определяются по формуле: х1,2 = (– В ± √Д) / 2 * А, где дискриминант Д равен: Д = В2 + 4 * А * С Определим Д: Д = (V1* r2 – V1* r1)2 + 4 * V22 * r2 * r1 = = V12 * (r2 – r1)2 + 4 * V22 * r2 * r1 = = V22 * r2 – 2 * V22 * r2 * r1 + r12 + 4 * V22 * r2 * r1 = = V22 * r2 + 2 * V22 * r2 * r1 + r12 = V12 * (r2 + r1)2 Найдём корни: V2 (1) = (V1 * r1 – V1 * r2 + V1 * (r2 + r1)) / 2 * r2 = = (V1 * r1 – V1 * r2 + V1 * r1 + V1 * r2) / 2 * r2 = V1 * r1 / r2 V2 (2) = (V1 * r1 – V1 * r2 – V1 * (r2 + r1)) / 2 * r2 = = (V1 * r1 – V1 * r2 – V1 * r1 – V1 * r2) / 2 * r2 = – V1 / 2 Второй корень (V2(2)) отбрасываем, т.к. линейная скорость (V1) – положительная по отношению к первоначальному направлению окружного движения. Тогда (V2 = V2 (1)), то есть V2 = V1 * (r1 / r2) (3.4.1) или V1 * r1 = V2 * r2 (3.4.2) Очевидно, что результаты этого расчёта справедливы, в том числе и для радиального движения к центру вращения. Меняется только знак работы ЦСС и знак приращения кинетической энергии тела. Таким образом, постоянная Кеплера определяется реальной внешней силой Кеплера, что противоречит аналогии закона сохранения углового момента с моментом сохранения импульса. Именно эта реальная сила Кеплера, проекция которой на перпендикуляр к радиусу совпадает с силой Кориолиса, и является физической основой явления Кориолиса. Для того чтобы различать силу Кеплера и классическую силу Кориолиса, но при этом сохранить обозначение их общей природы и историческую преемственность, мы предлагаем назвать проекцию силы Кеплера на перпендикуляр к радиусу – истинной силой Кориолиса-Кеплера. Это вполне реальная обычная сила, которая совпадает по направлению с силой Кориолиса, но в отличие от фиктивной силы инерции Кориолиса - реально изменяет импульс тела. Всё, что не связано с энергией самого вращения – является внешним для вращения, даже если это внутренняя энергия элементов самой конструкции вращающейся системы, но не задействованная непосредственно в механизме формирования вращения. Если работа внутренних сил вращающейся системы направлена на что то иное, помимо механизма вращения, то угловой момент не сохраняется. Например, в случае, когда сокращение радиуса происходит в результате наматывания нити на цилиндрическую ось исключительно только за счёт механизма вращения, т.е. за счёт внутренней энергии непосредственного самого вращения (см. Рис 3.4.3).
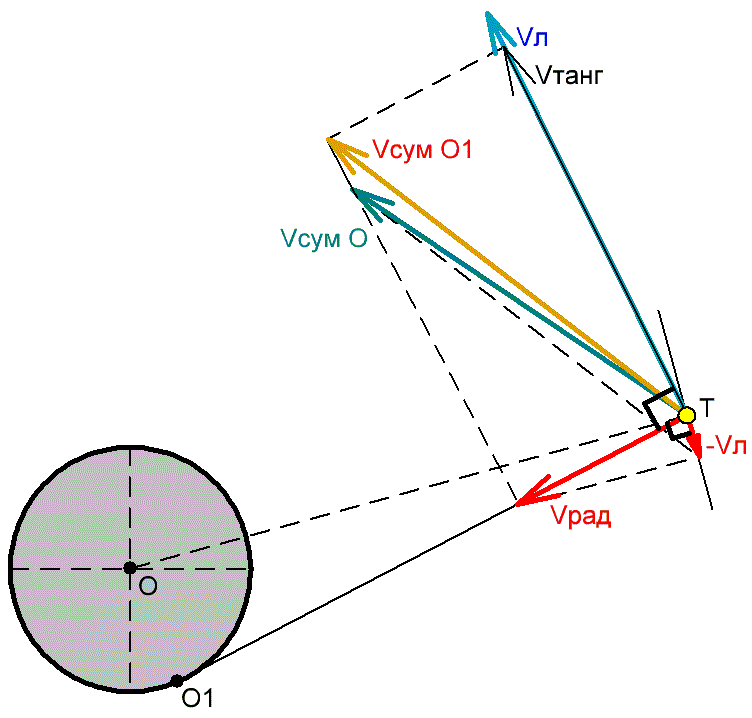
Рис 3.4.3 Точка (О1) на рисунке – это центр одного из вновь образуемых вращений с изменяющимся радиусом (ТО1) вдоль поверхности цилиндрической оси. Поскольку нить наматывается исключительно за счёт линейной скорости, то дополнительной энергии для увеличения линейной скорости в процессе сокращения радиуса просто нет. Поэтому при сокращении радиуса (ТО1) радиальная скорость (Vрад) может быть только частью линейной скорости (Vл). При этом тангенциальная скорость (Vтанг.) – это оставшаяся часть (Vл). При этом суммарная линейная скорость спирали с осью в точке (О1) – (Vсум О1) не может превысить линейную скорость Vл. На рисунке показано, что сумма (Vрад + V танг. = Vсум О1 = Vл). А с учётом потерь линейная скорость спирали (Vсум О1 < Vл). Кроме того, Vрад имеет отрицательную проекцию (-Vл) на касательную к окружности с радиусом (ОТ), т.е. относительно оси (О) суммарная линейная скорость (V сум О) будет ещё меньше, чем (Vсум О1). Задача определения любой тангенциальной силы вращательного движения с изменяющимся радиусом может быть успешно решена безо всяких моментов чего–то почему–то и связанных с ними парадоксов с помощью мерного радиана [мо]. Это будет показано в следующей главе (4.2.) на примере определения явных и неявных сил явления Кориолиса–Кеплера. | |
| Просмотров: 611 | |
| Всего комментариев: 0 | |