| Главная » Статьи » Физика и математика » Мои статьи |
Из приведённого выше описания механизма прецессии следует, что энергетически прецессия питается энергией внешней силы и энергией основного вращения, проявляющихся в одном взаимодействии. А поскольку сила взаимодействия для взаимодействующих тел является общей, то за истинную силу Кориолиса-Кеплера правомерно принять, как внешнюю силу, так и равную ей силу элементов (dm), т.е. собственно саму истинную силу Кориолиса-Кеплера. Обозначив запускающий прецессию момент сил Кеплера индексом (к), прецессию индексом (п), а момент импульса гироскопа индексом (г) можно записать: |МК| = dLГ / dt = |MП| = dLП / dt При этом, несмотря на расчёт вращения прецессии по её средним постоянным параметрам, мы фактически определяем только динамику пуска или останова псевдо равномерной старт-стопной прецессии. Для основного вращения гироскопа эта динамика его торможения. |MК| = |MП| = FK * r = mг * аK * r = mг * [Ωср * Vлг] * [r], Где: mг - усреднённая инертная масса гироскопа, участвующая в образовании усреднённых сил Кеплера, действующих в плоскости вращения прецессии Ωср - средняя скорость прецессии Vлг = ωср * r - средняя линейная скорость основного вращения гироскопа, здесь (ω * r) - угловая скорость и радиус основного вращения гироскопа соответственно Подставим в выражение для момента прецессии значение линейной скорости основного вращения гироскопа (VЛГ = ω * r): |МК| = |MП| = mг * [ω * r2 * Ωср] С учётом прямых углов между векторами [ω * r2 * Ω] в абсолютных величинах векторов получим: МК = MП = mг * ωср * r2 * Ωср Поскольку: LГ = mг * ωср * r2 то: МК = MП = LГ * Ωср Отсюда безо всяких парадоксов классического вывода угловой скорости прецессии гироскопа получаем: Ωср = (MП = MК) / LГ = MК / (I * ωср) Поведение прецессии подобно не скорости, а ускорению, которое прекращается с прекращением действия силы. Истинные силы Кориолиса-Кеплера объясняют и этот эффект кажущегося отсутствия инерционности прецессии безо всяких парадоксов. Вообще говоря, старт-стопное движение уже само по себе предусматривает преодоление инерции, как при разгоне, так и при торможении в каждом цикле движения. После прекращения действия внешней силы в гироскопе остаются только силы Кеплера, продолжающие действие во время его движения по инерции, которую никто не отменял. Вот эти истинные силы Кориолиса-Кеплера и преодолевают инерцию прецессии. Если мы снимем внешнюю силу во время цикла нутации, далеко от его завершения, то остановка будет длиться какое-то время, необходимое для завершения механизма остановки прецессии внутри цикла. Однако мы эту инерцию не заметим, т.к. в регулярной прецессии длительность циклов очень мала. Если же мы снимем внешнюю силу в конце цикла прецессии - нутации, то остановка прецессии будет выглядеть абсолютно безынерционной, т.к. сам процесс её остановки, происходящий внутри цикла, вообще останется для нас «за кадром». В классической физике отсутствие инерционности прецессии вектора (Lг) объясняется отсутствием его массы. Действительно, откуда у вектора масса, если это всего лишь математический символ? Но если в динамике вращательного движения твёрдого тела, когда вектор (LГ) изменяется по направлению, масса классической физике не нужна, то в динамике плоского вращения, когда вектор (LГ) изменяется по абсолютной величине, он почему то вдруг приобретает вполне реальную массу. Несмотря на маразм классической физики с безмассовым вектором (Lг) затраты энергии как на остановку прецессии, так и на её запуск реально существуют, что принципиально не возможно без массы, свойствами которой собственно и определяется всё, что происходит в природе. В некотором приближении можно даже оценить количественно гипотетическую гироскопическую (mПГ) массу прецессии, которая хотя подкреплена силами, но базируется на реальной массе гироскопа (mг). МК = MП = LГ * Ωср или mпг * (dΩ / dt) * после сокращения на (r2) получим: mпг * dΩ / dt = mг * ωср * Ωср Поскольку при разгоне и торможении прецессии её угловая скорость изменяется от нуля до (Ωmax) и обратно, то приращение угловой скорости прецессии в полуцикле равно (dΩ = Ωmax). Тогда, учитывая, что (Ωmax = 2 * Ωср) получим: mпг * 2 * Ωср / dt = mг * ωср * Ωср Отсюда: mпг = mг * ωср * dt / 2 Пусть, например, (ω = 10000 об/с = 62800 рад), а полупериод нутации (dt = 0, 01с), тогда: mпг = 314 * mг Это означает, что в этом конкретном примере истинные силы Кориолиса эквивалентны увеличению инерционности прецессии в 314 раз по сравнению с физической массой гироскопа. То есть, как только мы уберём внешнюю силу, то через (0,01 с) прецессия остановится за счёт возросшей в 314 раз эквивалентной массы прецессии. Такое же сопротивление, очевидно, проявляется и при запуске прецессии. Причём резкую остановку прецессии после снятия внешней силы, можно объяснить возросшей инерционностью прецессии за счёт сил Кеплера, что эквивалентно возросшей гироскопической массе самого гироскопа. В динамике плоского вращения, например, классическая физика подобным образом объясняет изменение сопротивления вращению в зависимости от радиуса. Поэтому массу в динамике вращательного движения заменяет момент инерции. В гироскопе радиус так же изменяется, но не по абсолютной величине, а в соответствии с изменением плоскости вращения. Однако в отличие от плоского вращения классическая физика видит в прецессии не увеличение массы, а, наоборот её исчезновение. А вообще все эти классические вольности с самым фундаментальным понятием в природе массой недопустимы даже условно академически, т.к. это уводит науку в сторону от реальной действительности. Современная наука просто обязана отличать внешнее сопротивление от массовой инертности. Постоянная средняя скорость установившейся прецессии в некотором смысле подобна линейной скорости равномерного вращательного движения в нашей модели вращательного движения, в том смысле, что она поддерживается на постоянном уровне за счёт разнонаправленных тангенциальных ускорений. Однако инерция вращательного движения всегда заметна. Колебания его линейной скорости в отличие от колебания линейной скорости прецессии никогда не достигают нулевой величины. Поэтому после снятия центростремительной силы, т.е. фактически связи с центром вращения, движение не останавливается. В отличие от равномерного вращательного движения, в котором «нутации» не отнимают энергию вращения, в гироскопе нутации уменьшают энергию основного вращения гироскопа. Выводы:
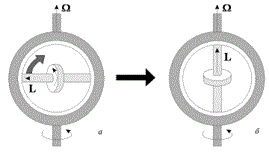
1. Прецессия гироскопа осуществляется за счёт энергии внешних сил, запускающих прецессию и за счёт внутренней кинетической энергии основного вращения гироскопа, которая питает реальные истинные силы Кориолиса-Кеплера. 2. Старт-стопный режим прецессии не предполагает возвратно поступательного движения энергии, подводимой внешней силой, как это происходит в циклах равномерного вращательного движения или свободных колебаниях упругого тела. Прецессия - энергетически затратный процесс. 3. Прецессия не является безынерционной, как утверждает классическая физика. Инерция — это явление, лежащее в основе всех без исключения взаимодействий. Инерция прецессии гасится истинными силами Кориолиса в каждом цикле её формирования. Поэтому после снятия внешней силы прецессия прекращается в течение одного цикла. Поскольку нутации - циклы прецессии достаточно малы, то инерционность движения инертных масс гироскопа мало заметна на макроуровне. 4. Нутация гироскопа не прекращаются до тех пор, пока осуществляется прецессия, т.к. нутация это суть и циклы прецессии. *** Направление гироскопических сил можно найти с помощью правила, сформулированного Н.Е. Жуковским: гироскопические силы стремятся совместить момент импульса L гироскопа с направлением угловой скорости вынужденного поворота. Это правило можно наглядно продемонстрировать с помощью устройства, представленного на рис. (4.7.7).
Ось гироскопа закреплена в кольце, которое может свободно поворачиваться в обойме. Приведем обойму во вращение вокруг вертикальной оси с угловой скоростью Ω (вынужденный поворот). При этом кольцо с гироскопом будет поворачиваться в обойме до тех пор, пока направления L и Ω не совпадут. Такой эффект лежит в основе известного магнитомеханического явления - намагничивания железного стержня при его вращении вокруг собственной оси - при этом спины электронов выстраиваются вдоль оси стержня (опыт Барнетта).
| |
| Просмотров: 1211 | |
| Всего комментариев: 0 | |