| Главная » Статьи » Физика и математика » Мои статьи |
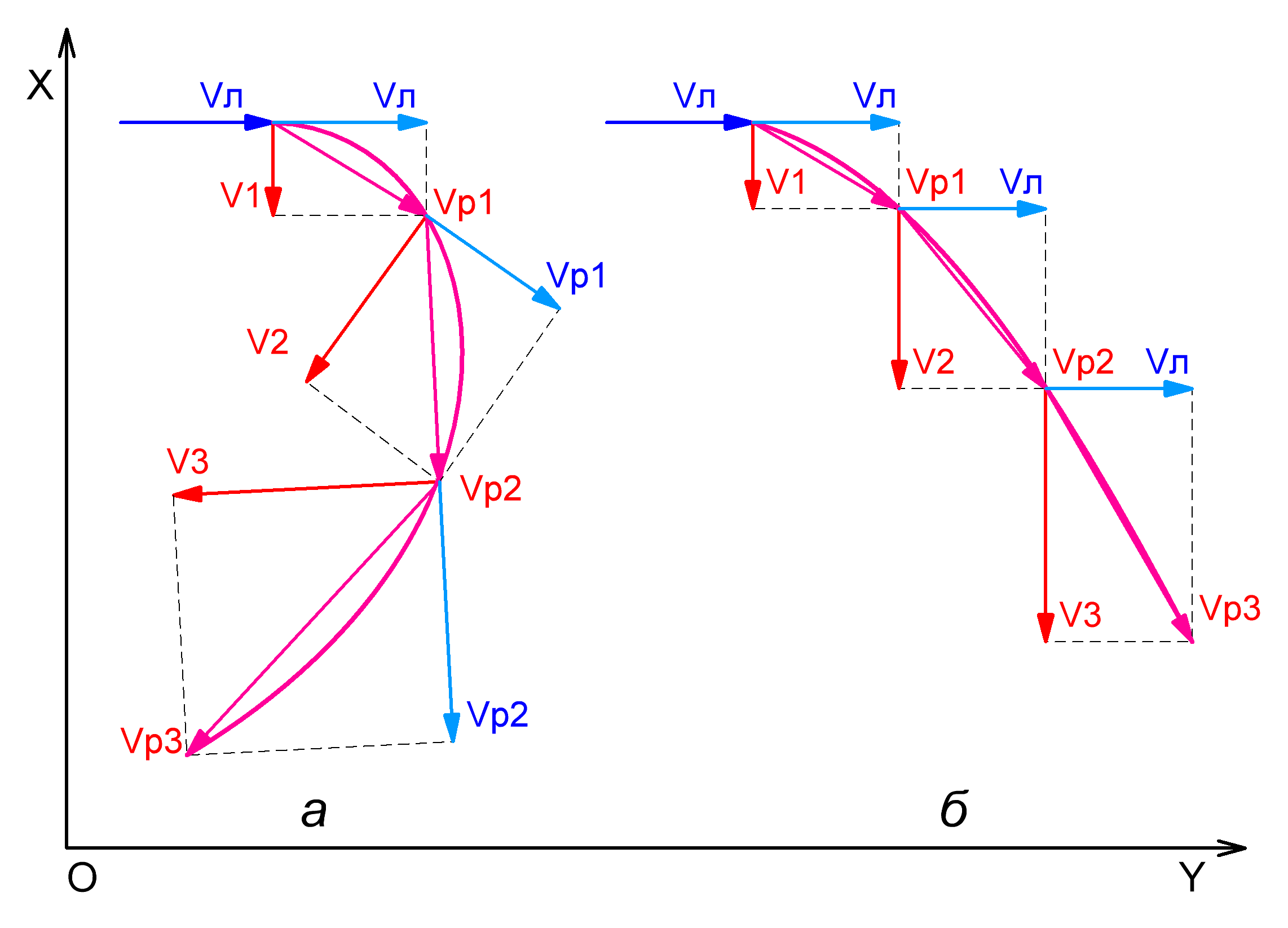
С точки зрения классической физики основной причиной образования вращательного движения (ВД) является центростремительная сила (ЦСС) и вызываемое ей центростремительное ускорение (ЦСУ), которые якобы изменяют направление вектора линейной скорости движущегося по окружности тела без изменения его величины. Однако это противоречит таким фундаментальным понятиям и определениям классической физики, как второму закону Ньютона, правилу сложения векторов, а также классической динамике вращательного движения (ДВД). Начнём с официальных понятий и определений. Ускорение — векторная величина, характеризующая быстроту изменения скорости точки по численному значению и по направлению. Второй закон Ньютона в его наиболее распространённой формулировке: в инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, не зависит от её природы, совпадает с ней по направлению и обратно пропорционально массе материальной точки. Угловая скорость — векторная величина, характеризующая быстроту и направление вращения материальной точки или абсолютно твёрдого тела относительно центра вращения. Изменение скорости по направлению – это поворот вектора скорости на некоторый угол за некоторое время. Осуществляется с угловой скоростью. Направление угловой скорости: Если головка правого винта совпадает с направлением вращения, то поступательное движение острия покажет направление вектора угловой скорости. Направление углового ускорения: Вектор углового ускорения ускоренного вращения со направлен с вектором угловой скорости, а равнозамедленного – противонаправлен угловой скорости. Рассмотрим упомянутые выше противоречия более подробно. 1. В соответствии со вторым законом Ньютона вектор ускорения должен совпадать с направлением вызывающей его силы. Формально ЦСУ, направленное к центру вращения удовлетворяет этому условию. Однако при этом поступательное перемещение в направлении действия ЦСС отсутствует, что противоречит самому принципу движения, как перемещения в пространстве, в том числе и за счёт вращения. К тому же в соответствии с оригинальной трактовкой 2-го ЗН движущая сила должна изменять количество движения в направлении своего действия (Исаак Ньютон, Математические начала натуральной философии, под редакцией Л.С. Полака, перевод с латинского и комментарии А.Н. Крылова, МОСКВА "Наука", 1989 г.): "Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует. Если какая-нибудь сила производит некоторое количество движения, то двойная сила произведет двойное, тройная—тройное, будут ли они приложены разом все вместе, или же последовательно и постепенно. Это количество движения, которое всегда происходит по тому же направлению, как и производящая его сила, если тело уже находилось в движении, при совпадении направлений прилагается к количеству движения тела, бывшему ранее, при противоположности — вычитается, при наклонности — прилагается наклонно и соединяется с бывшим ранее, сообразно величине и направлению каждого из них.» Как видно, никаких исключений к наклонности в 900 Ньютон не делает. Сложите бывшее движение с новым движением под 900 и вы получите результирующее движение в обоих этих направлениях, в том числе и в направлении под 900 к бывшему движению! По определению вектор ЦСУ показывает не направление движения тела, а направление поворота вектора его скорости. Однако и это утверждение не лишёно противоречий. Момент ЦСС, приложенной к центру масс (ЦМ) тела, равен нулю, что исключает поворот самого тела, который к тому же не является изменением направления движения самого тела в целом в виде изменения направления движения его ЦМ. Поворот вектора скорости возможен только через сложение приращения прежнего движения с приращением движения в ином направлении, которое и есть поступательное перемещение в направлении силы, вызывающей поворот. Поворот движения вне пространственного перемещения в сторону поворота не возможен в принципе, как не возможно и само движение вне пространства. Таким образом, классическое понятие ЦСУ одновременно противоречит, как ДВД, так и КМН и в частности второму закону Ньютона! Поворота тела при воздействии ЦС силы строго на его ЦМ не может быть в принципе, как не может быть в принципе и поворота движения тела вне его поступательного перемещения в направлении действия силы и ускорения, а поступательное приращение движения в направлении поворота противоречит ЦСУ. В реальной действительности тело во вращательном движении не только изменяет направление своего движения без итогового изменения величины скорости, но и реально поворачивается вокруг своей оси, что свидетельствует о наличии множества разнонаправленных и разновеликих сил, причастных к физическому механизму образования ЦСУ и ВД. 2. В классических определениях ЦСУ и угловой скорости заложен абсолютно идентичный физический смысл, чего не может быть в принципе. Текст совпадает даже буквально: ЦСУ — нормальная составляющая ускорения тела, характеризующая быстроту изменения направления (вращения) вектора скорости. Угловая скорость — псевдовекторная величина, характеризующая быстроту и направление вращения (изменения направления). Как видно, оба эти определения одинаково характеризуют быстроту и направление вращения. Однако двух истин не может быть в принципе. Скорость и ускорение - это разные понятия. Поэтому они не могут иметь абсолютно идентичные определения! И это вовсе не случайность. Это свидетельствует о серьёзных противоречиях, как в классической механике Ньютона, так и в классической динамике вращательного движения, а также их противоречии между собой. Так, например, ЦСУ, которое в механике Ньютона отвечает исключительно только за направление, измеряется вовсе не в единицах направления (углового перемещения), а в линейных единицах [м / с2], что является количественной оценкой изменения именно длины пространства во времени и в частности поступательного перемещения в направлении ЦСС и ЦСУ, как реального физического ускорения (позже мы узнаем, что ЦСУ — не физическое ускорение). Это также свидетельствует о том, что преобразование скорости по направлению эквивалентно её количественному преобразованию в новом направлении, что не возможно без поступательного перемещения в пространстве вдоль направления силы. Однако в классической физике поступательное перемещение в направлении ЦСУ категорически отрицается. А вот в ДВД угловое ускорение измеряется именно в угловых единицах! И направлено оно не вдоль силы, как обычное линейное ускорение, а вдоль оси вращения. То есть это так же, как и угловая скорость — псевдовекторная величина, которая противоречит ЦСУ по своему физическому смыслу. Подробнее противоречия классической механики Ньютона и классической динамики вращательного движения будут рассмотрены в главе (3.4.2.). 3. Во всех учебниках механики Ньютона центростремительное ускорение выводится через разностный вектор скорости (приращение скорости), который определяется через реальное линейное приращение движения в направлении действия силы (см. например, О. Ф. Кабардин «ФИЗИКА» МОСКВА «ПРОСВЕЩЕНИЕ» 1991 и др.). Как известно, движение принципиально не может осуществляться вне пространства. Таким образом, классические выводы ЦСУ противоречат классической же модели вращательного движения, в которой отсутствует поступательное перемещение в направлении ЦСС и ЦСУ, а также физическому смыслу движения материи в пространстве, что мы уже отмечали выше. 4. ЦСС, как собственно и любая другая сила, не может совершать работу в отсутствие перемещения в направлении своего действия. То есть в соответствии с классическими представлениями о ЦСУ, работа ЦСС в отсутствие линейного перемещения должна быть равна нулю. Но отсутствие действия (работы) силы в отношении ускоренного движения эквивалентно отсутствию самой силы и вызываемого ей ускорения, что соответствует исключительно равномерному и прямолинейному движению. Таким образом, классическая модель вращательного движения (ЦСС и ЦСУ) просто физически не может быть причастно к вращательному движению, т.к. реальное действие силы не может осуществляться без работы этой силы, что равносильно отсутствию силы. Однако при этом классическая физика категорически отрицает причастность равномерного вращательного движения к первому закону Ньютона. 5. Отсутствие линейного приращения движения в направлении ЦСС при достижении прямого угла между V и ЦСС противоречит правилу сложения векторов и законам природы, которые оно отражает. Прямой угол ничем принципиально не отличается от любых других углов, при которых линейное поступательное приращение движения при сложении векторов не подлежит ни малейшему сомнению в самой же классической физике. Кроме того, даже если абсолютная величина скорости после изменения её направления в конечном итоге не изменяется, то в новом направлении оказывается перестроенной её прежняя абсолютная величина, что не возможно без пространственного приращения движения в полном соответствии со вторым законом Ньютона, который сформулирован безотносительно к углу приложения силы относительно вектора скорости тела. Принципиальное наличие поступательного перемещения в направлении физического ускорения не может зависеть от угла приложения силы к направлению движения. Это противоречит не только второму закону Ньютона, но и понятию движения в принципе. Физически процесс преобразования движения по направлению без изменения в конечном итоге абсолютной величины его скорости можно упрощенно проиллюстрировать на примере отражения. При взаимодействии с отражающей поверхностью перпендикулярная к ней составляющая скорости движения тела сначала уменьшается до нуля, а затем изменяет свое направление на противоположное. В результате абсолютная величина скорости тела в направлении падения сначала уменьшается, а затем вновь восстанавливается до прежнего значения, но уже в новом направлении отражения. Таким образом, абсолютная величина скорости при изменении её направления после отражения в конечном итоге не изменяется, однако изменение направления скорости происходит через преобразование её абсолютной величины в новом направлении. Нечто подобное, очевидно, происходит и в равномерном вращательном движении. Поскольку абсолютная величина линейной скорости вращательного движения после изменения её направления остаётся неизменной, что не возможно осуществить при однократном точеном взаимодействии, которое принципиально осуществляются только вдоль прямой линии, то наряду с механизмом изменения скорости по направлению необходим ещё и механизм регуляции её абсолютной величины, как это происходит в механизме отражения. Совершенно очевидно, что одно только центростремительное ускорение, якобы отвечающее исключительно только за изменение направления, не может обеспечить этот механизм ни в части изменения направления, ни в части сохранения величины скорости. В соответствии с классической моделью вращательного движения центростремительное ускорение образуется под действием силы упругости связующего тела, направленной нормально к вектору линейной скорости. Естественно, что при этом центростремительная сила не может иметь проекции на ортогональное себе направление, вдоль которого направлен вектор линейной скорости. Из этого классическая физика делает вывод, что нормальное ускорение обеспечивает приращение скорости только по направлению! Однако тело может испытывать ускорение только вдоль линии действия внешней силы, если внешнее воздействие либо совпадает с линией существующего движения тела, либо осуществляется вдоль линии, проходящей через центр масс неподвижного тела. В противном случае тело будет испытывать ускорение в направлении действия мгновенной результирующей силы, равной геометрической сумме сил инерции поэлементной поддержки, внешней силы, проявляющейся в направлении предыдущего движения тела, если таковая имеется, и внешней силы, возмущающей существующее движение. Напомним, что внутренняя сила инерции поэлементной поддержки является такой же реальной силой, как и любые внешние силы, приложенные к телу (см. гл. 1.2.1). На рис. (3.1.1 а) показана траектория, по которой будет двигаться тело, если постоянное ускорение в составе достигнутого за счет этого ускорения движения (V1, V2, V3) в каждый текущий момент времени занимает перпендикулярное положение по отношению к каждой текущей результирующей скорости (Vр1, Vр2, Vр3). При этом источник силы движется синхронно с телом в направлении каждого нового результирующего движения. Как видно из рисунка, такое сложение двух движений не обеспечивает неизменность результирующего вектора линейной скорости (Vр1, Vр2, Vр3) по абсолютной величине. При этом с изменением направления вектора результирующей скорости одновременно изменяется и его абсолютная величина. Траектория такого движения не только далека от окружности, но даже не является замкнутой кривой. Это движение по спирали. Рис. 3.1.1 На рис. (3.1.1 б) показана кривая, по которой будет двигаться тело, если постоянное ускорение в составе достигнутого за счет этого ускорения движения (V1, V2, V3) в каждый текущий момент времени неизменно занимает перпендикулярное положение по отношению к неизменному по величине и по направлению исходному вектору линейной скорости (Vл). При этом источник силы движется в исходном направлении с такой же по абсолютной величине скоростью. Исходный вектор при этом естественно не вращается, т.к. это всего лишь проекция реального движения на одно и то же неизменное направление! А результирующая скорость за счет вертикальной составляющей изменяется как по величине, так и по направлению. Однако это опять же не замкнутая кривая. Это классический случай движения тела, брошенного горизонтально относительно поверхности Земли, описанный практически во всех учебниках физики. Траектория такого движения представляет собой параболу. Таким образом, при любом внешнем воздействии, осуществляющемся под любым не равным нулю углом к направлению прежнего движения, в том числе и под прямым углом, который не является каким–либо исключением из этого правила, изменяется не только направление скорости результирующего движения, но и ее величина. Совершенно очевидно, что в реальной действительности в равномерном вращательном движении существует, как механизм изменения скорости по направлению, так и по величине. В классической модели равномерного вращательного движения радиальное движение отсутствует, даже, несмотря на действие вполне реальной неуравновешенной центростремительной силы. При этом окружное движение осуществляется с постоянной скоростью. Это означает, что ускоренное перемещение в равномерном вращательном движении отсутствует также и в тангенциальном направлении, т.е. полное абсолютное ускорение равно нулю! Следовательно, центростремительная сила не может быть неуравновешенной. А уравновесить её может только не фиктивная сила, а вполне реальная центробежная сила инерции поэлементной поддержки в периоды ослабления ЦСС в соответствии с механизмом образования вращательного движения. Причём, как показано выше, под каким бы углом к вектору скорости тела ни была бы направлена периодицески неуравновешенная ЦСС, тело в соответствии со вторым законом Ньютона не может изменять направление своего движения, не совершая при этом ускоренного поступательного перемещения в направлении её действия.
Во-первых, одна сила - это вовсе не момент сил и поэтому одиночная сила не умеет ничего вращать без поступательного перемещения. А, во-вторых, криволинейных сил в природе не бывает, поэтому одна только прямолинейная сила не может ничего двигать криволинейно. Для этого необходим соответствующий алгоритм и механизм взаимодействия с участием множества сил.
В соответствии со вторым законом Ньютона под воздействием ЦСС в нормальном к линейной скорости направлении непременно должно зарождаться новое движение с нормальным ускорением. Но по правилам векторной геометрии, в основе которых лежат законы природы, при сложении вновь образующегося нормального вектора скорости с существующей линейной скоростью, результирующий вектор скорости непременно должен изменяться не только по направлению, но и по абсолютной величине. Кроме того, в соответствии со вторым законом Ньютона все изменения скорости должны происходить ускоренно. Однако, как это ни странно для самого понятия «ускорение», но в равномерном вращательном движении вектор линейной скорости изменяется по направлению, хоть и с центростремительным ускорением, но не ускоренно, а равномерно! Следовательно, либо второй закон Ньютона на вращательное движение не распространяется, чего не может быть в принципе, либо центростремительному ускорению в равномерном вращательном движении что–то реально противодействует. И это «что–то» вовсе не фиктивное. Если центростремительная сила упругости отклоняет вектор линейной скорости в сторону центра вращения с одновременным увеличением его абсолютной величины, то в дальнейшем центробежная сила инерции отклоняет его в обратную сторону с одновременным уменьшением его абсолютной величины точно на такую же величину, как и ЦС сила. В противном случае никакого равномерного изменения вектора скорости по направлению в сторону центра вращения без изменения его абсолютной величины просто не получится. Далее начинается новый цикл механизма формирования вращательного движения. При новом «падении» на новую «отражающую поверхность» вновь происходит уменьшение абсолютной величины вектора линейной скорости с отклонением его от центра вращения. А при новом «отражении» вновь происходит восстановление абсолютной величины вектора линейной скорости с одновременным изменением его направления к центру. Таким образом, с учётом реальности центробежной силы инерции, которая во вращательном движении проявляется в соответствии с механизмом инерции поэлементной поддержки, все парадоксы классической модели равномерного вращательного движения разрешаются естественным образом, без каких–либо противоречий с законами Ньютона. Вращательное движение является внутренним движением тела или системы диаметрально противоположных тел, если осуществляется строго в границах тела или системы тел и не связано с ускоренным перемещением тела или системы тел в пространстве. При этом ЦБ и ЦС силы диаметрально уравновешивают друг друга. Для отдельно взятой точки, равномерно движущейся по круговой траектории, уравновешивающее действие диаметрально противоположного тела отсутствует. Поэтому с классической точки зрения равномерное движение отдельно взятого тела по круговой траектории вне вращающейся системы возможно только под действием неуравновешенной силы. Однако это верно только отчасти, поскольку такое действие не непрерывно. Равномерное движение отдельной точки по окружности возможно только за счёт того же самого механизма преобразования движения по направлению, как и в связанном вращении. Другой физической причины у вращательного движения просто нет. Поэтому активная центростремительная сила, действующая на лишённую связующего тела и диаметрального противовеса точку, должна так же, как и в связанном вращении периодически уступать отвоёванное ей во всех направлениях пространство силе инерции поэлементной поддержки, ослабляя своё воздействие. Такое периодически изменяющееся равновесие активной силы упругости и силы инерции поэлементной поддержки и приводит к отклонению точки к центру окружности, т.к. направление движения всегда изменяется в сторону силы, действующей последней. При этом возникает полная иллюзия неуравновешенной внешней центростремительной силы упругости, направленной на центр окружности (подробнее см. гл. 3.2.1.). А обобщённую академическую величину ЦСУ, усредняющую в своём составе бесконечное множество разновеликих и разнонаправленных ускорений, также можно условно академически приравнять к физическому ускорению, направленному в сторону указанного отклонения, т.е. на центр окружности. Центробежная сила инерции поэлементной поддержки, растягивая связующего тело, реально совершает работу по преодолению силы упругости связующего тела. Естественно, что скорость инерционного движения тела при этом уменьшается, т.к. она преобразуется в напряжение связующего тела, характеризующееся его силой упругости. После изменения направления движения в сторону центра вращения работу по возвращению вращающегося тела к центру вращения совершает уже центростремительная сила, восстанавливая таким образом линейную скорость. Таким образом, классическое центростремительное ускорение равномерного вращательного движения это не «мгновенное» физическое ускорение в направлении центра вращения, а обобщённая академическая величина, представляющая собой косвенную энергетическую оценку процесса преобразования движения по направлению. Эта величина обобщает все мгновенные разновеликие центростремительные и центробежные ускорения равномерного вращательного движения, которые проявляются во всех направлениях процесса преобразования движения по направлению. Очевидно, что направление линейной скорости на макроуровне изменяется не дискретно. Каким бы ни был малым рассматриваемый интервал времени, ЦСУ имеет в этом интервале бесконечное множество мгновенных направлений. Поэтому классический разностный вектор (ΔV), который определяется только по двум дискретным (фиксированным) положениям, не соответствует полной энергетике равномерного вращательного движения. *** | |
| Просмотров: 2607 | Комментарии: 6 | |
| Всего комментариев: 6 | |
|
| |