| Главная » Статьи » Физика и математика » Мои статьи |
В классической физике равномерное вращательное движение считается не равноускоренным движением. Например, авторы статьи «Вращательное движение. Равномерное движение точки по окружности. Вектор угловой скорости. Угловое ускорение Д. А. Паршин, Г. Г. Зегря (https://docplayer.ru/53379680-Lekciya-3-vrashchatelnoe-dvizhenie-ravnomernoe-dvizhenie-tochki-po-okruzhnosti-vektor-uglovoy-skorosti-uglovoe-uskorenie.html), утверждают, что равномерное движение по окружности не является равноускоренным, цитата: «Пример плоского неравноускоренного движения, известный вам из школьного курса физики, это равномерное движение по окружности». Однако, как же тогда расценивать тот факт, что ускорение такого «неравноускоренного» движения является величиной постоянной? Тем более что преобразование скорости по направлению эквивалентно её количественному преобразованию в новом направлении. Величина постоянного центростремительного ускорения также измеряется вовсе не в единицах направления (углового перемещения), а точно в таких же единицах, в которых измеряется и абсолютная величина ускорения. При этом принцип равномерности изменения любой величины для всех один и характеризуется постоянной величиной изменения. Таким образом, в классической физике налицо парадоксальная ситуация, когда криволинейное движение с постоянной по модулю и равномерно изменяющейся по направлению скоростью считается не равноускоренным движением только потому, что это движение не прямолинейное! Кроме того, центростремительное ускорение точно так же, как и ускорение равноускоренного прямолинейного движения со 100% точностью можно определить простым делением приращения скорости на время этого приращения, не прибегая к операции дифференцирования, что является верным признаком исключительно только равномерного и равноускоренного движения. За один полный оборот годограф линейной скорости равен длине окружности радиуса (V): ∆V = 2 * π * V Время, за которое вектор линейной скорости совершат полный оборот равно: t = 2 * π / ω Тогда ускорение по изменению направления можно определить, как частное от деления приращения направления на время этого приращения. ан = 2 * π * V / (2 * π / ω) = V * ω или с учетом ω = V / R: ан = V2 / R Для (n) оборотов соответственно имеем: ∆V = 2 * π * V * n t = (2 * π /ω) * n ан = 2 * π * V * Как видно, центростремительное ускорение равномерного вращательного движения не зависит от величины интервала, в котором оно определяется. Величину центростремительного ускорения можно получить аналитически еще одним способом, не прибегая к дифференцированию.
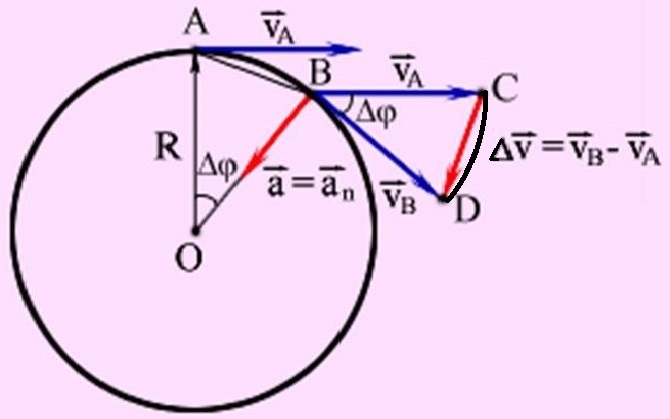
Рис. 3.1.2 На рисунке (3.1.2) показано изменение направления линейной скорости при круговом движении в направлении от точки (А) к точке (В). Как известно угловая скорость вращения (ω) равна частному от деления линейной скорости (Vа) на радиус (R): ω = Vа / R (3.1.1) Линейная скорость движения по дуге окружности (СD) с радиусом (Vа), которая в фактически и является центростремительным ускорением или ускорением направления в нашей версии (ан), равна: ан = ω * Vа (3.1.2) Очевидно, что угловая скорость вращения радиуса (ОА) равна угловой скорости вращения вектора (Vа), поскольку они участвуют в одном и том же равномерном вращательном движении. Тогда подставляя в формулу (3.1.2) выражение для угловой скорости (ω=V/R) получим классическое выражение для центростремительного ускорения: ан = Vа2 / R (3.1.3) Как видно никакого дифференцирования для определения величины центростремительного ускорения якобы неравноускоренного равномерного вращательного движения не потребовалось и в этом случае, что характерно только для равноускоренного движения. Один из главных парадоксов классической модели вращательного движения состоит в том, что абсолютно правильный количественный результат центростремительного ускорения получен в классической физике приближённым методом дифференцирования не правильно определённого приращения вращательного движения (∆V). Этот парадокс связан с простой подменой понятий истинного приращения равномерного вращательного движения в виде его годографа на классический разностный вектор (∆V). Классический вывод формулы центростремительного ускорения (см. Рис. 17, О. Ф. Кабардин «ФИЗИКА» МОСКВА «ПРОСВЕЩЕНИЕ» 1991 или Рис. 3.1.2), основан на анализе соотношения сторон подобных треугольников (АОВ) и (СВД). В малом интервале времени стороны (АВ) и (СД) в этих треугольниках мало отличаются от соответствующих им одноимённых дуг окружности, которые опираются на стороны (АВ) и (СД) как на хорды. Поэтому в классическом выводе формулы центростремительного ускорения стороны треугольников (АВ) и (СД) в пропорции (R/(V*∆t) ≈ V/∆V (см. Рис. 3.1.2)) фактически подменяются одноимёнными дугами, т.е. реальным годографом линейной скорости и пропорциональным ему годографом радиус–вектора рассматриваемого вращательного движения. Из этой пропорции получают: а = ∆v / ∆t = v 2 / R Таким образом, в выводе, представленном Кабардиным, формула центростремительного ускорения фактически выводится не из подобия треугольников, а из подобия фигур (АОВ) и (СВД) стороны (АВ) и (СД), которых являются дугами окружности. При этом если рассматривать приращение равномерного вращательного движения (СД), как дугу вместо хорды, всё становится на свои места естественным образом. Знак примерного равенства в пропорции (R/(V*∆t) ≈ V/∆V) естественным образом заменяется знаком абсолютного равенства. Таким образом, если равномерное вращательное движение является ускоренным движением, то оно именно равноускоренное движение. Направление центростремительного ускорения объясняется якобы стремлением разностного вектора на центр вращения в бесконечно малом интервале времени. Однако бесконечное стремление никогда не достигает цели, на то оно и бесконечное. К тому же строго на центр разностный вектор будет направлен при (∆t = 0), когда нечего собственно будет и направлять, т.к. он сам при этом станет равен нулю. Таким образом, направление центростремительного ускорения на центр вращения в представлении классической физики является полной бессмыслицей, которая не имеет под собой физического обоснования. Это подтверждается также другим классическим обоснованием направления центростремительного ускорения, приведённое в учебнике физики для 9 класса, которое не только противоречит физическому смыслу реальной природы обобщённого центростремительного ускорения, но и приведённому выше классическому же обоснованию: "Пользуясь правилом треугольника, совместим начала векторов и проведем красным цветом вектор разности (правый чертеж). Как видите, вектор разности скоростей, а, значит, и сонаправленный с ним вектор ускорения спутника направлен к центру окружности». («Физика–9", Тема 13, «Введение в кинематику», § 13–л. «Центростремительное ускорение».)
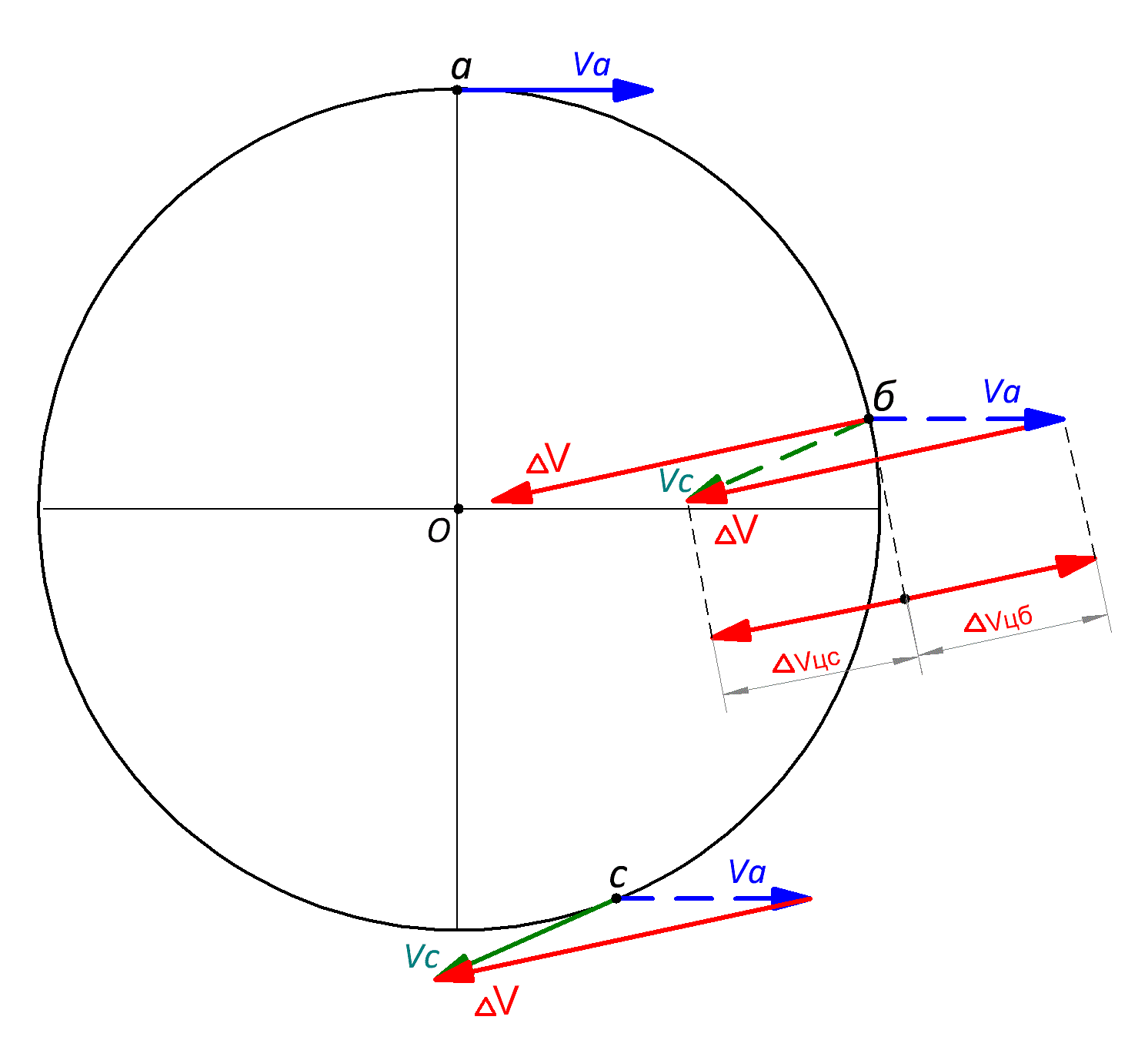
Таким образом, авторы учебника физики для 9 класса перехитрили даже классическую физику. У них центростремительное ускорение направлено на центр вращения в любом сколь угодно большом в пределах полуокружности интервале времени, если конечно же, перенести разностный вектор в центрально симметричную точку между векторами. Причём авторы учебника, сами того не подозревая, фактически подтвердили не центростремительное ускорение, а НЕУДАЛЕНИЕ тела от центра вращения. Авторы Физики 9 определяют разностный вектор вовсе не по классической векторной геометрии, которая сравнивает вектора в одной из выбранных точек, как это сделано, например у Кабардина (см. Рис. 3.1.2), а в центральной точке, расположенной строго по середине между разными направлениями вектора линейной скорости. Это эквивалентно центральной точке цикла формирования вращательного движения, в которой ускорения нет. В ней есть только равновесие не удаления от центра и не приближения к нему. В результате, благодаря полной симметрии выбранных точек относительно центральной точки между ними, а также полной симметрии отклонения векторов от центра окружности по сравнению с центральной точкой, но с разными знаками, суммарное отклонение взаимно компенсируется, т.е. равно нулю. Однако у авторов Физики 9 разностный вектор не равен нулю и направлен на центр вращения, т.к. они не учли разные знаки отклонения векторов скорости от центральной точки и соответственно подменили два разнонаправленных вектора ЦС и ЦБ ускорения одним классическим ЦС ускорением. Исправим их ошибку (см. Рис. 3.1.3). На рисунке (3.1.3) показаны вектора скоростей (Va) и (Vc) на приращении (ас), равном без малого половине окружности. При этом без учёта знаков отклонения разностный вектор (∆V) в центральной точке (b) направлен строго на центр вращения безо всякой минимизации интервала дифференцирования. Однако по правилам векторной геометрии векторы на отрезке (ас) должны сравниваться либо в точке (а), либо в точке (с). При этом никакого направления на центр без минимизации интервала дифференцирования не получится. Разностный вектор в точке (с), например, вообще не попадает в окружность.
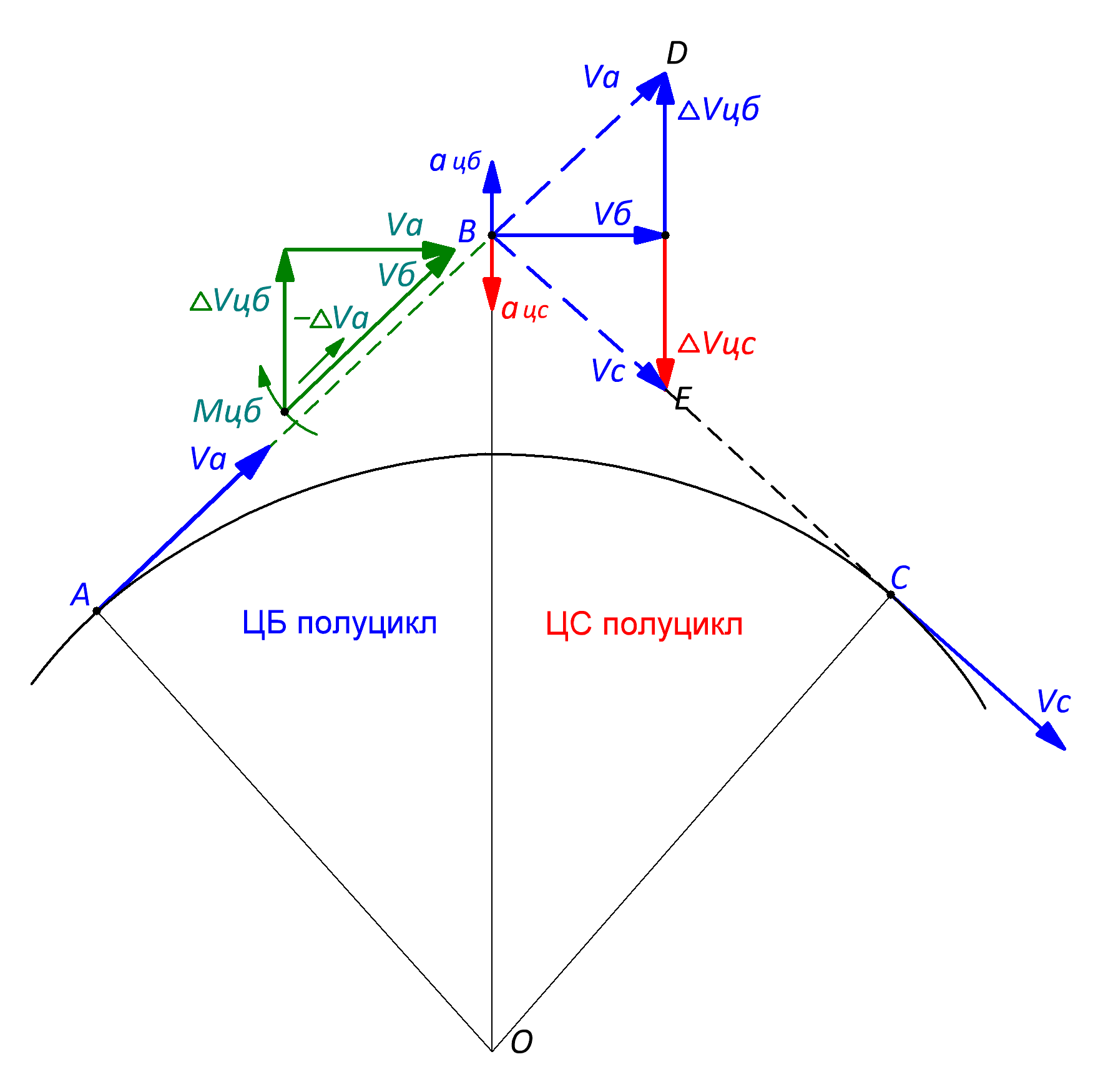
Рис. 3.1.3 Центральная точка (б) на (Рис. 3.1.3) эквивалентна центральной точке полного цикла формирования вращательного движения, который более подробно показан на (Рис. 3.1.4). В соответствии с механизмом инерции поэлементной поддержки уже остановленные было силой упругости связующего тела элементы вращающегося тела, вновь ускоряются за счёт вновь присоединяемых к нему пока ещё не остановленных элементов. При этом радиальная составляющая скорости вновь присоединяемых элементов, с которой классическая физика связывает направление своих абстрактных векторов сил, направлена от центра вращения. Соответственно в этом же направлении проявляется и вполне реальное центробежное ускорение (см. ЦБ полуцикл).
Рис. 3.1.14 Причём ничего принципиально нового в инерции поэлементной поддержки для классической физики нет. Вспомните, как трогается с места тяжёлый железнодорожный состав. Сначала локомотив сдаёт назад, выбирая зазоры в сцепках, а затем, последовательно разгоняя в пределах зазоров каждый вагон по отдельности, легко страгивает с места весь тяжёлый состав. Теперь, если мы начнём останавливать уже движущийся состав, начиная с последнего вагона, то получим наглядную модель реальной центробежной силы инерции поэлементной поддержки и реального центробежного ускорения. Остановленный последний вагон – это первый присоединённый элемент. А роль вновь присоединяемых элементов играют последующие вагоны, которые последовательно передают уже остановленным элементам–вагонам свою ещё неизрасходованную в пределах своих зазоров порцию движения. При этом все уже присоединённые элементы движутся во внешнем радиальном направлении с центробежным ускорением. Однако поскольку энергия этого движения берётся из запаса инерционного движения тела, общая скорость удаления всего тела от центра уменьшается, а направление её вектора приближается к касательной в точке (B). В середине цикла формирования равномерного вращательного движения, когда к телу в новом направлении присоединится последний элемент вращающегося тела, его активное радиальное удаление от центра вращения заканчивается. При этом вектор скорости (Vа) займёт перпендикулярное положение к связующему телу, превратившись в вектор скорости (Vв) в точке (В). Причём, как показано выше, поворот вектора скорости (Vа) в ЦБ полуцикле происходит вовсе не за счёт центростремительного ускорения, а за счёт реального центробежного ускорения инерции поэлементной поддержки. А вот во втором центростремительном полуцикле на участке (ВС) всё происходит уже за счёт центростремительной силы и соответственно центростремительного ускорения. При этом, поскольку во втором полуцикле центростремительное ускорение проявляется в попутном направлении с движением тела, то его скорость (Vc) будет увеличиваться и полностью восстановится до величины исходного вектора (Vа), но теперь уже вдоль касательной в точке (С). При этом среднее ускорение каждого цикла равно нулю. Абсолютная величина академического центростремительного ускорения, как энергетическая характеристика преобразования движения по направлению, определяется в нашей версии также, как и в классическом выводе, т.к. треугольники, а точнее фигуры (АСО) и (BDE), остаются подобными и в нашей версии (см. Рис. 3.1.4). При этом в качестве (∆V) необходимо учитывать сумму абсолютных значений двух разнонаправленных векторов (∆V). Однако для скалярных величин, каковыми в нашей версии является сила и ускорение, это не принципиально. На рисунке (3.1.4) стрелки (ацб) и (ацс) – это лишь направление скорости развития процессов. Из представленного выше механизма инерции поэлементной поддержки следует, что момент центробежной силы инерции поэлементной поддержки приложен к задним ближним к связующему телу элементам, останавливаемым в первую очередь. Это означает, что поворот вектора (VA) осуществляется относительно его стрелки, как центра поворота. За счёт центробежной силы, образно говоря, происходит всем хорошо известный занос «автомобиля» с задним приводом. Поэтому на протяжении всего поворота разностный вектор (∆Vцб) направлен от центра вращения (см. отдельный фрагмент зелёного цвета на Рис. 3.1.4). В классической физике все тела заменены материальной точкой центра масс тела. При этом любые повороты векторов, начинающихся в точке центра масс соответственно осуществляются относительно их тупых концов. Поэтому стрелка классического разностного вектора (∆Vцб) на протяжении всего поворота стремится к направлению на центр вращения. Это и есть одно из объяснений классического направления ускорения равномерного вращательного движения. Однако вектор это всего лишь условное академическое обозначение весьма ограниченных классических представлений о развитии взаимодействий. Классическая физика представляет общее напряжение взаимодействия в виде двух абстрактных разнонаправленных векторов сил. При этом, как показано в главе (1.2.1.), в реале общее для всех взаимодействующих тел напряжение взаимодействия есть величина скалярная, а за направление скалярных сил и ускорений в классической физике академически принимается направление скорости ответного тела.
| |
| Просмотров: 1153 | |
| Всего комментариев: 0 | |