| Главная » Статьи » Физика и математика » Мои статьи |
Довольно странный вывод. На самом деле во всей физике нет ничего более существенного, чем основной закон природы - закон сохранения материи, который в выводе Эйнштейна подвергается вопиющему нарушению в виде прямого перехода массы-материи в нематериальную лучистую энергию. Причём это голословное заявление Эйнштейна непосредственно в выводе ни из чего не следует. Объективно масса излучателя уменьшается по причине потери масс двух фотонов. Однако Эйнштейн без всяких на то оснований ассоциирует энергию двух излучённых по условию вывода фотонов L, не просто с их массой, а с массой всего лишь одного из двух излученных фотонов. Действительно: L = m * c2 = 2Lф Тогда: Lф = mф * c2 / 2 L / c2 = 2 * mф или L / c2 = m2ф Из этого следует, что энергия соответствует старой доброй ньютоновской формуле. Формула Эйнштейна Е = m * c2 несостоятельна. Вообще говоря, формально формулу релятивисткой энергии Эйнштейн получил уже в предшествующей работе «К электродинамике движущихся тел», Берн, Швейцария, от 30 июня 1905 г: W = m * c2 * (1 / корень (1 - v2 / c2) - 1) В приведённом выводе Эйнштейн утверждает, что «разность Kо - K1 зависит от скорости точно так же, как кинетическая энергия электрона». Тогда после подстановки вместо L → m * c2 и аппроксимации получим: Ко - К1 = L / c2 * v2 / 2 = Ко - К1 = m * c2 / c2 * v2 / 2 = m * v2 / 2 Выражение m * c2, полученное Эйнштейном из ньютоновской энергии через тавтологию преобразований Лоренца-Эйнштейна вновь приводит релятивистскую кинетическую энергию к ньютоновской формуле. Причём вовсе не потому, что релятивистская формула энергии единственно верная. Искусственно подогнанный под преобразования Галилея и постулаты Эйнштейна релятивистский корень уже содержит в себе релятивистскую энергию. Естественно, что при обратном преобразовании через аппроксимацию бинома Ньютона вновь проявляется заранее заложенное, что и есть тавтология. Именно в квадратном корне релятивистского коэффициента сначала прячется, а затем при обратном преобразовании вновь появляется коэффициент «½». Причём в англоязычной Википедии в статье Correspondence principle в параграфе Relativistic kinetic energy этот ловкий фокус приведён в качестве подтверждения верности релятивисткой формулы энергии. Есть такой фокус и в наших учебниках: «Уравнение Лоренца можно записать в форме Mр = Mо (1 - v2 / c2) -1/2. Используем аппроксимацию для |х| <<1: (1 + х) n ≈ 1 + x * n Тогда: Мр = Мо + 1/2 * Mо * v2 / c2 Обозначим энергию через Е, тогда: Mр = Mо + Е / c2 ∆M = Мр - Мо = Е / c2 Обозначим ∆M = m Тогда Е = m * c2» Здесь наглядно показано, как из релятивистского корня сначала получается ньютоновская энергия Е, а затем та же самая Е ловко превращается в релятивистскую энергию уже безо всякой аппроксимации. Вот только вначале в обозначенной через Е энергии была масса покоя Мо, а затем в той же самой Е она вдруг превратилась в приращение массы ∆M = m, что кстати не соответствует даже СТО. Если это полная энергия Еп = Мр * c2, то в ней масса релятивистская Мр. Е = 1/2 * Mо v2 = m * c2 = ∆M * c2 Как вам такое художество, в котором простым обозначением ньютоновская энергия удваивается и превращается в релятивистскую?! Ничуть не лучше, чем в оригинальном выводе Эйнштейна, в котором удваивается масса, что так же эквивалентно получению формулы Эйнштейна через мошенническое удвоение ньютоновской энергии. Как видите, ни в одном из представленных выводов не обошлось без мошенничества и тавтологии. Врать стали все с лёгкой руки главного шарлатана Эйнштейна. «Но что ни говори, он добрый малый; в особенности восхищает меня та ловкость, которая стяжала ему репутацию великого умника. Я говорю о его манере отрицать то, что есть, и распространяться о том, чего не существует». Эдгар По Один из наших оппонентов утверждает, что формула Эйнштейна не имеет никакого отношения к обычным телам. Это всего лишь выражение скорости ЭМ волны, через плотность энергии (w) и массовую плотность ЭМ поля (р). Он исходил из того, что формула скорости распространения ЭМ волны следует из теории упругости сплошной среды: v = корень (G / p), где G: модуль сдвига. Переходя к скорости света якобы получаем: с = корень (w / p), где W якобы равна G, т.е. (w = G). Оппонент сослался, что последнее равенство следует из классической физики, он в него особо не вникал, но доверился классике. В итоге получаем энергию ЭМ волны: W = m * c2 Мы же решили вникнуть в это дело поглубже и вот что из этого получилось: Начнём с модуля сдвига. Итак, модуль сдвига (G) из Википедии:
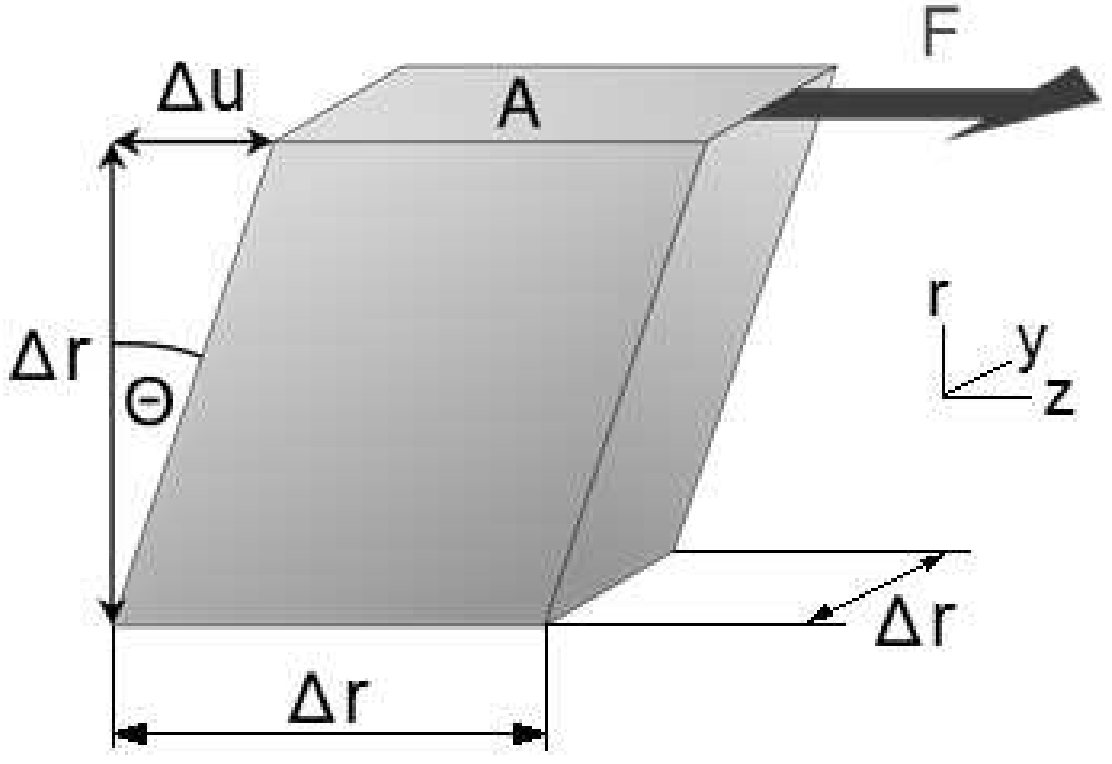
Рис. Из Википедии. «G = τ / ɣ = (F / A) / (∆u / ∆r) = (F * ∆r) / (A * ∆u) Скорость поперечной волны зависит от модуля сдвига: с = Корень (G / p) где р: массовая плотность среды». Теперь выясним правомерность равенства (w = G). Пусть энергия сдвига возбуждает энергию поля, и соответственно энергию волны. Остаётся определить эту энергию. Итак, энергия сдвига, поля и волны равна работе силы (F) на усреднённом участке от (0) до (∆u), т.е. на участке (∆u / 2) (см. Рис. из Википедии) равна: W = ½ * (F * ∆u) ∆u = ɣ * ∆r F = τ * ∆r2 Тогда: W = ½ * (τ * ∆r2 * ∆u) Определим плотность энергии при (V = A * ∆r = ∆r3): w = W / V = ½ (τ * ∆r2 * ∆u)/r3 = ½ (τ * ∆u / ∆r) Умножим правую часть на τ / τ: w = ½ (τ * τ * ∆u / ( τ * ∆r)) Заметим, что ∆u / (τ * ∆r) = 1 / G Тогда: w = ½ (τ2 / G) Отсюда: G = ½ (τ2 / w) Как видите, (G) это вовсе не то же самое, что плотность энергии (w). Во всяком случае при чистом сдвиге обычного упругого тела. С учётом (G) получим: c2 = ½ (τ2 / (w * p)) Очевидно, что из этого формулу Эйнштейна не слепишь ни для фотонов, ни для ЭМ волны, ни для обычных тел. А теперь посмотрим, что можно действительно слепить из последнего выражения. Умножим правую часть на (V / V = ∆r3 / ∆r3): c2 = ½ (τ2 * ∆r3/ (w * p * ∆r3)) = ½ (F2 * ∆r3/∆r4) / (w * m) = ½ (F2/∆r) / (w * m) c2 = ½ (F2 /∆r) / (w * m) Ещё раз умножим правую часть на (V / V = ∆r3 / ∆r3): c2 = ½ (F2 * ∆r2) / (W * m) = ½ W2/ (W * m) = ½ W / m или c2 = ½ W / m, Отсюда окончательно получаем нормальную формулу энергии (W) из нормальной классической механики: W = m * c2 / 2 Модуль сдвига измеряется в единицах силы, отнесённой к единицам площади - паскалях, что при полном раскрытии всех физических величин, входящих в модуль сдвига, формально совпадает с размерностью плотности энергии. Однако энергия - это вовсе не сила, отнесённая к единице площади. Энергия в единичном объёме не перестаёт быть энергией в Джоулях на метр объёма ([дж/моб.). Следовательно, физически модуль сдвига не соответствует плотности энергии. А энергия обычных тел не может отличаться от энергии фотонов или ЭМ-волны, если в основе и того, и другого лежит одна и та же материя.
| |
| Просмотров: 452 | |
| Всего комментариев: 0 | |