| Главная » Статьи » Физика и математика » Мои статьи |
Вращение тел в небесной механике. Фундаментальные законы природы, если они верны, должны выполняться в любой точке мирового пространства. Поэтому законы вращательного движения должны выполняться и на Земле и в космосе. Однако в небесной механике необходимо учитывать специфику движения тел в поле тяготения. Космические объекты, как правило, тела протяженные. Их в еще большей степени, чем обычные тела нельзя рассматривать как материальные точки. Заменяя реальные физические тела материальными точками можно выявить лишь наиболее общие закономерности, не раскрыв физической сущности явления.
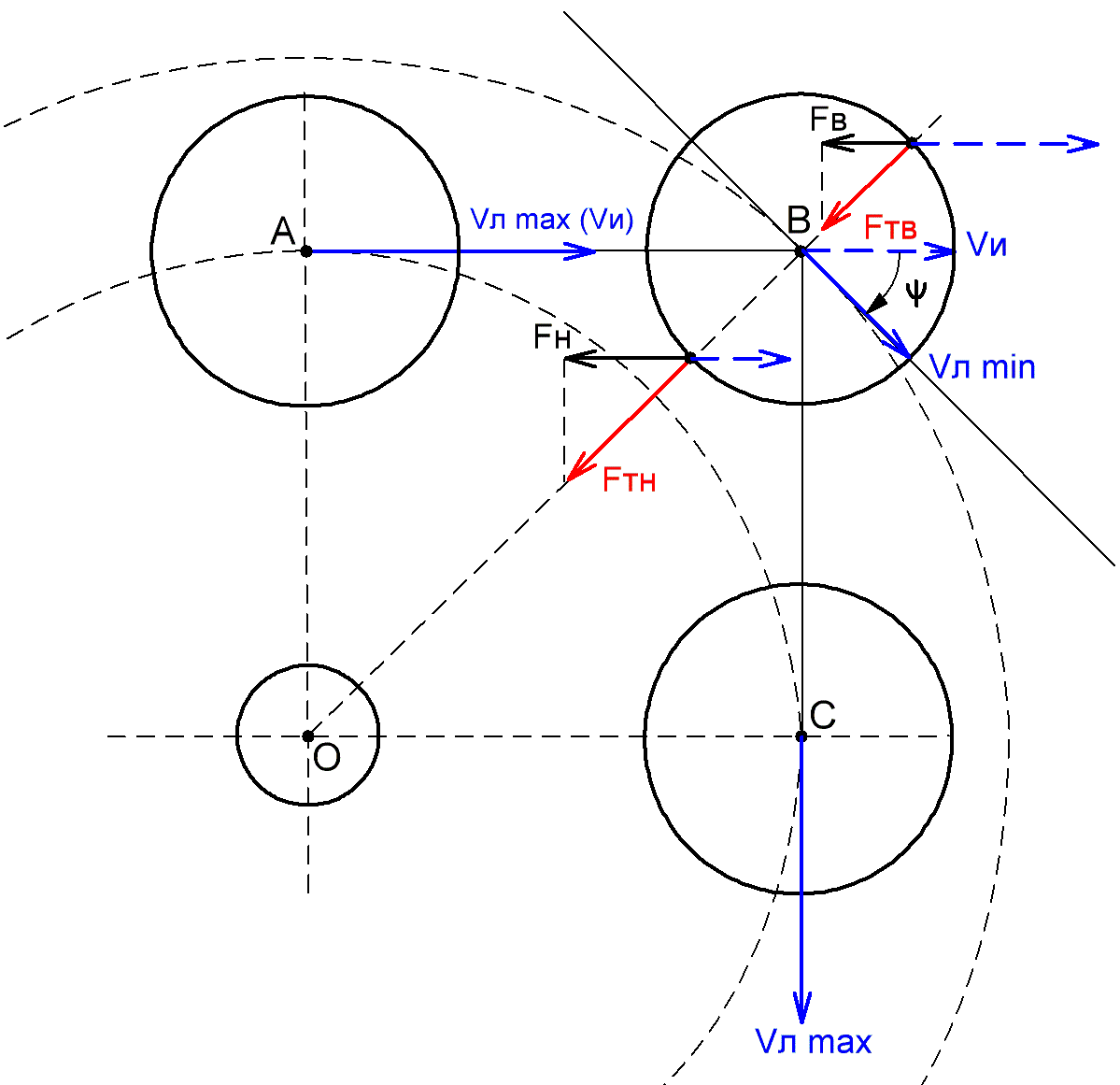
Рис. 3.3.1 На Рис. 3.3.1 графически пояснен физический механизм движения тела по круговой орбите в небесной механике в нашем видении. На нижнюю и верхнюю часть небесного тела действует сила тяготения (Fтн) и (Fтв) соответственно. Очевидно, что нижняя часть тела испытывает большую силу тяготения, чем верхняя за счет разницы расстояний до центра тяготения. Проекции этих сил (Fн) и (Fв) на направление линейной скорости уменьшают инерционную скорость (Vи), причем нижние точки тела будут замедляться сильнее верхних точек. Это эквивалентно появлению закручивающих сил («момента» сил), который приводит к повороту движения тела в сторону центра тяготения и уменьшению угла (ψ) между вектором линейной скорости и касательной к окружности с текущим радиусом. В результате, радиальное удаление тела от центра тяготения в какой-то момент прекращается, после чего начинается движение тела в сторону центра вращения. При этом под действием ускорения тяготения линейная скорость тела начнет увеличиваться. На нижней орбите в точке (С) величина линейной скорости восстанавливается до исходного значения в точке (А). При этом движение осуществляется вдоль касательной к нижней орбите в точке (С). Далее весь процесс повторяется. Таким образом, прослеживается полная аналогия механизма движения тел в поле тяготения с механизмом движения по окружности обычных тел, связанных с центром вращения связующим телом. Однако есть и отличия, обусловленные заменой силы упругости связующего тела в жестко связанном вращении, силой тяготения в небесной механике. В жестко связанном вращении связующее тело механически ограничивает радиальное движение вращающегося тела. Поэтому процесс преобразования движения по направлению осуществляется на микроуровне. В небесной механике механических ограничений на уровне физических тел нет. Сила тяготения очень слаба по сравнению с силой контактного взаимодействия. К тому же с увеличением расстояния она убывает. Поэтому она не может погасить инерцию линейного движения тела в прежнем направлении на микроуровне. По этим причинам орбитальный пробег тела (АВ) и (ВС), а также радиальные колебания (ВД) внутри цикла формирования вращательного движения в небесной механике должны обнаруживаться на макроуровне. Установим хотя бы оценочный размер этих величин. Если мы внимательно посмотрим на рисунок, то увидим, что (ВД) это есть не что иное, как отклонение от траектории вращательного движения, т.е. девиация вращательного движения.
3.3.1. Физический смысл девиации в физике. Девиа́ция (от лат, deviatio — отклонение). В физике девиация применяется для определения ускорения точки на траектории. Для этого измеряют отклонение и время отклонения точки от своего места на траектории ускоренного движения в предположении, что в какой-то момент точка перестаёт ускоряться, двигаясь дальше только с постоянной, достигнутой на этот момент скоростью. Ускорение точки на траектории через девиацию определяется по формуле пути, пройденного с ускорением без начальной скорости (а = 2 * S / t2), т.к. в момент схода с траектории скорости отклонившейся точки и её места на траектории, продолжающего своё прежнее движение, равны. При этом за направление ускорения принимается направление на новое место точки на траектории. Это и есть ошибочная классическая академическая модель девиации, которая отличается от естественной природной девиации. В природной девиации, благодаря явлению инерции, тело отклоняется от заданной траектории не с нулевым ускорением. Нет в природной девиации и движения по касательной. Отклонение и возврат на заданную траекторию с ненулевым ускорением осуществляется по криволинейным траекториям. На участке образования отклонения происходит уменьшение прежнего ускорения по величине и его изменение по направлению, а затем осуществляется возврат на заданную траекторию с приобретением ускорения в новом направлении. Полное ускорение движения соответствует усреднённой величине всех ускорений проявляющихся в полном цикле изменения движения. В идеале естественная природная девиация осуществляется в равномерном вращательном движении, которое фактически состоит из симметричных отражений между условными окружностями наименьшего и наибольшего удаления тела от центра вращения (см. главу 3.2.). При этом центростремительное ускорение соответствует усреднённой величине всех ускорений проявляющихся в полном законченном цикле формирования равномерного вращательного движения. В произвольном криволинейном движении механизм природной девиации принципиально тот же, что и в равномерном вращательном движении. Однако в нём происходит наложение друг на друга отражений с разными параметрами, которые и теоретически, и практически учесть очень сложно. Поэтому для упрощения определения абсолютного ускорения произвольного движения в нашей версии (см. гл. 7.3) участок девиации необходимо минимизировать по правилам дифференцирования, в котором все параметры движения фактически усредняются, что сводит произвольное криволинейное движение на этом участке к равномерному вращательному движению, а его ускорение к центростремительному ускорению. В классической физике абсолютное ускорение произвольного криволинейного движения ошибочно определяется многими методами, в том числе и в соответствии с ошибочной академической девиацией. При этом, если с условным направлением центростремительного ускорения, в том числе и в качестве полного ускорения произвольного движения в некотором смысле можно согласиться, то направление классического абсолютного ускорения произвольного движения, не совпадающее с главной нормалью, грубо нарушает нормы природной девиации. Подробнее определение ускорения произвольного криволинейного движения через природную девиацию, т.е. через равномерное вращательное движение будет рассмотрено в главе (7.3.). Таким образом, природной основой девиации в физике является физический механизм отражения, определяющий равномерное вращательное движение, которое является природным измерительным эталоном произвольного криволинейного движения (подробнее см. гл. 7.3.). *** А теперь вернёмся непосредственно к нашим расчётам. Поскольку оценочный расчёт всегда достаточно грубый, то условно примем, что скорость в цикле по абсолютной величине изменяется незначительно. Поэтому мы и обозначили её как инерционную скорость (Vи). Для того чтобы, хотя бы приблизительно оценить параметры цикла преобразования движения по направлению в небесной механике, нам осталось только оценить время цикла. Это мы можем сделать пока только интуитивно. Наверное, для того чтобы повернуть спутник, движущийся с первой космической скоростью (Vи = 7,9 км /с) даже на небольшой угол (ѱ), понадобится, на наш взгляд, никак не менее секунды. Выбора у нас пока нет, поэтому для оценочного расчёта пусть будет 1 секунда. Мы приняли, что скорость изменяется незначительно. Однако принципиально природная девиация, хотя и определяется одним отклонением (ВД), но измеряется в оба конца, т.к. центростремительное ускорение обобщает все ускорения в цикле. Тогда: S = 2 * ВД = g * t2 / 2 = 5 [м] Отсюда: ВД = S / 2 = 2,5 м Пробег спутника (АВ) в полуцикле, т.е. за 0,5 секунды примерно равен: АВ = Vи * t = 3950 [м] Как видно это вполне поддающиеся измерению величины! Даже если мы ошиблись со временем в 100 раз, то (ВД) и (АВ) не перестанут быть величинами доступными для измерения современными средствами. Пусть t = 0, 01c: ВД = S / 2 = а * t2 / 4 = 0, 00025 [м] АВ = V1 * t = 7900 * 0,01 = 79 [м] Осталось выполнить соответствующие измерения на орбите, что вполне доступно современной науке, и тогда наша модель вращательного движения будет или подтверждена или опровергнута. А пока таких измерений нет, данные приведённого оценочного расчёта будем считать гипотезой, ожидающей своей проверки. В жестко связанном вращении центростремительное ускорение в значительной степени характеризуется статическим напряжением остаточной деформации связующего тела. Поэтому рассчитать геометрические размеры параметров его цикла достаточно сложно. Тем не менее, такие величины так же доступны для измерения современной науке. Только никто и никогда этим не занимался, т.к. всех устраивает классическая абстрактная модель вращательного движения. *** Как было показано выше форма траектории движения обычных тел, связанных с центром вращения связующим телом зависит от добротности вращающейся системы. Наиболее стабильным является движение по круговой траектории, которое соответствует наибольшей добротности вращающейся системы. В небесной механике форма орбиты также зависит от добротности вращающейся системы. Однако в отсутствии связующего тела добротность вращающейся системы в небесной механике определяется не жесткостью связующего тела, а степенью соответствия начальной линейной скорости движения, требуемой линейной скорости движения по круговой орбите для каждого фиксированного расстояния до центра тяготения. Чем больше начальная линейная скорость движения небесного тела соответствует линейной скорости движения по круговой орбите на данном расстоянии до центра тяготения, тем выше добротность вращающейся системы в небесной механике и наоборот. Для Земли скорость движения по круговой орбите в непосредственной близости от её поверхности соответствует первой космической скорости и равна 7,9 км/с. Движение по орбите со скоростью, отличающейся от расчётной скорости движения по круговой орбите, имеет более низкую добротность. При начальной скорости движения у поверхности Земли больше первой космической (но не более 11,2 км/с для Земли) тело будет двигаться по эллиптической траектории. Наконец при некоторой исходной скорости тело может полностью преодолеть силу тяготения. Это вторая космическая скорость, которая у поверхности Земли составляет 11,2 км/с. Расчётная скорость круговой орбиты определяется массами взаимодействующих небесных тел и квадратом расстояния между ними. Из закона всемирного тяготения следует, что ускорение свободного падения не зависит от массы падающего тела. Однако, на наш взгляд, это выполняется только для несопоставимых по величине масс, когда (М>> m). Для соизмеримых масс (М=m) величина силы тяготения на одном и том же расстоянии между телами, возможно, будет отличаться от величины силы тяготения между несоизмеримыми массами, что может быть обусловлено зависимостью гравитационной постоянной от соотношения масс взаимодействующих тел при одном и том же значении их произведения. Если это так, то ускорение свободного падения также зависит от соотношения масс взаимодействующих тел. С уменьшением соотношения масс гравитационная постоянная, по нашему мнению, должна уменьшаться. Она так же должна уменьшаться и при сопоставимых, но очень малых по сравнению с небесными телами массах. Предлагаемый механизм вращательного движения может в виде гипотезы ответить на вопрос, почему в космосе за редким исключением стабильные орбиты имеют в основном крупные небесные тела. По нашему мнению, это происходит, потому что для малых объектов из–за малых размеров действие силы тяготения на дальние и ближние от центра тяготения точки мало различается по величине. В результате возникновение поворотного момента сил затруднено и действие его не достаточно эффективно. При недостаточном повороте линейная скорость малых небесных тел более эффективно гасится силой тяготения, как во вращающихся системах с низкой добротностью, и небесные тела, в конце концов, падают к центру тяготения, либо удаляются от центрального тела безвозвратно, если их начальная скорость достаточно велика. На этом специфика вращательного движения в небесной механике не заканчивается. Поворот обычных тел относительно собственного центра масс в процессе движения по окружности происходит в условиях механического ограничения со стороны связующего тела. В результате поворот тела движущегося по круговой орбите составляет один оборот вокруг собственной оси на один оборот вокруг центра кругового движения. В небесной механике такой поворот обеспечивает сам механизм вращения тел в небесной механике, в соответствии с которым ближние к центральному тяготеющему телу части вращающегося тела тормозятся сильнее дальних (см. Рис. 3.3.1 и пояснения к нему). Однако поскольку небесное тело не имеет жесткой связи с центром тяготения, то нет и жестких ограничений при вращении вокруг собственной оси, если это вызвано, например, какими-либо внешними причинами что, по всей видимости, может привести к дестабилизации орбитального движения. Собственное вращение тела увеличивает орбитальную скорость удаленных от центрального тяготеющего тела точек движущегося по орбите тела, где сила тяготения сказывается меньше и уменьшает орбитальную скорость нижних точек, где сила тяготения сказывается сильнее. В результате собственное вращение небесных тел может привести к снижению их орбиты и медленному падению на центральное тяготеющее тело, т.к. удаление от центрального тяготеющего тела верхних точек, движущегося по орбите тела, не может скомпенсировать падения на центральное тело нижних его точек. Кроме того, скорость обтекания эфирным потоком верхней части вращающегося в прямом направлении тела вокруг собственной оси ниже, чем скорость обтекания нижней части тела, т.к. линейная скорость верхних точек тела направлена навстречу общему потоку эфира, возникающему при круговом движении, а линейная скорость нижних точек совпадает с направлением потока. При этом, если скорость собственного вращения достаточно велика, то это также приводит к падению тела на центральное тело. Все планеты Солнечной системы и само Солнце вращаются в одном и том же (прямом) направлении. Так же вращаются и большинство спутников за исключением группы малых спутников Юпитера (VIII, IX и XII), спутник Феб Сатурна и Тритон Нептуна. Они имеют не прямое, а обратное вращение. Но это скорее исключение требующее специальных исследований. Свое вращение большинство тел Солнечной системы, конечно же, получили не в результате захвата одного небесного тела другим, а в ходе образования Солнечной системы, которая, по-видимому, образовывалась из единого вращающегося газового облака. В результате все небесные тела и орбиты закручены в одну сторону. Собственное вращение небесных тел, движущихся по орбитам относительно центрального тяготеющего тела, может привести к дестабилизации Солнечной системы. Однако существует и обратный процесс, противодействующий дестабилизации. Линейная скорость верхней части тела, движущейся по внешней орбите выше чем линейная скорость нижней части тела, движущейся по внутренней орбите. При этом возникает подъемная сила в виде градиента давления эфира, направленного наружу. Тело поднимается на более высокую орбиту. При торможении эфиром скорость тела падает, но за счёт ускорения свободного падения скорость тела вновь возрастает и оно переходит на нижнюю орбиту. Затем процесс такой стабилизации бесконечно повторяется. Для небольших небесных тел из-за малого диаметра, беспорядочного вращения и неправильной формы воздействие мировой среды, по-видимому, неэффективно, поэтому в указанном противодействии побеждают силы тяготения. В результате малые тела быстрее снижаются к центральному тяготеющему телу. Но это лишь гипотеза. В современной науке этот вопрос остается открытым. Таким образом, движение небесных тел зависит от множества факторов, что в некоторых случаях приводит к отклонению от закона всемирного тяготения Ньютона, который применим в основном для математических материальных точек и усреднённому для тел любой массы взаимодействию между собой через посредничество мировой материальной среды. Однако это посредничество зависит, как от соотношения масс, так и от их абсолютной величины, т.к. зависимость изменения мировой материальной среды от этих факторов, по всей видимости, не линейная. Когда французский математик Анри Пуанкаре попробовал исследовать стабильность планетной системы, опираясь лишь на законы Ньютона, он был поражен. Получалось, что Солнечная система была нестабильна и в самой основе своей хаотической. Одним из объяснений причин нестабильности и отклонения движения небесных тел от законов всемирного тяготения может быть пренебрежение теорией реальными размерами тел и замена их математическими материальными точками. К сожалению, в научной литературе этот вопрос не достаточно освещен, хотя задуматься есть над чем. Подробнее см. А. А. Астахов "Физика движения", глава 3.4; 12.4 | |
| Просмотров: 1861 | |
| Всего комментариев: 0 | |