| Главная » Статьи » Физика и математика » Мои статьи |
Механизм формирования вращательного движения. Для образования вращательного движения тело должно иметь инерцию прямолинейного движения. То есть необходимо разогнать покоящееся тело (В) до какой-то скорости прямолинейного движения (Vп), которая в дальнейшем в процессе преобразования прямолинейного движения во вращательное движение приобретет значение линейной скорости вращения (Vл) - (см. Рис. 3.2.1). Движущееся прямолинейно тело соединим связующим телом с центром вращения. Пусть центр вращения зафиксирован в пространстве, чтобы не смешивать при рассмотрении вращательного движения непосредственно вращение и прямолинейное движение. В противном случае тело получит смешанное сложное движения вместе с центром вращения.
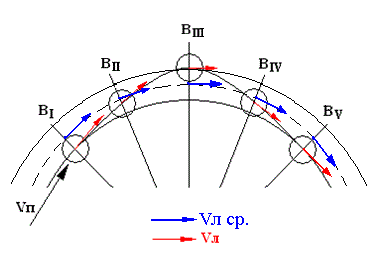
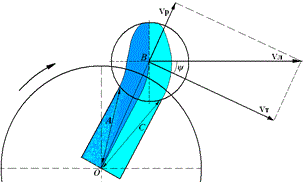
Рис. 3.2.1 На Рис. 3.2.1 условно изображены пять фаз процесса изменения направления движения тела (В) во вращательном движении: начало, середина и окончание цикла преобразования движения по направлению, а также по одной промежуточной фазе в каждом полуцикле. Фазы обозначены римскими цифрами (I, II, III, IV, V). Сплошной линией обозначены граничные круговые траектории с минимальным и максимальным растяжением связующего тела. Пунктирная линия обозначает среднюю круговую траекторию, которая и наблюдается в общей кинематике вращательного движения. В первой фазе происходит «захват» движущегося прямолинейно тела (В) со скоростью (Vп) связующим телом. В этот момент инерция движения тела максимальна, а сила реакции нерастянутого связующего тела минимальна. В фазах с первой по третью расстояния (А) и (С) увеличиваются (см. Рис. 3.2.1, 3.2.2), т.к. тело удаляется от центра будущего вращения. Поскольку тело имеет некоторую протяженность в направлении линейной скорости, то расстояние (С) всегда больше расстояния (А). Следовательно, передняя по ходу движения часть области сопряжения растягивается сильнее, чем задняя, что соответствует изгибу. Таким образом, в связующем теле постепенно накапливается упругая деформация двух видов. Это растянутая деформация, образующаяся за счет общего удлинения связующего тела и изгибная деформация, образующаяся за счет разницы расстояний (А) и (С). Растянутая деформация распределяется по всей длине связующего тела. Изгибная деформация накапливается в основном непосредственно в области сопряжения тела со связующим телом. Границы деформации условно обозначены на рисунке 3.2.2 разным цветом. В левой части области деформации (синий цвет) накапливается «малое» растяжение, в то время как, в правой части (бирюзовый цвет) – растяжение большое.
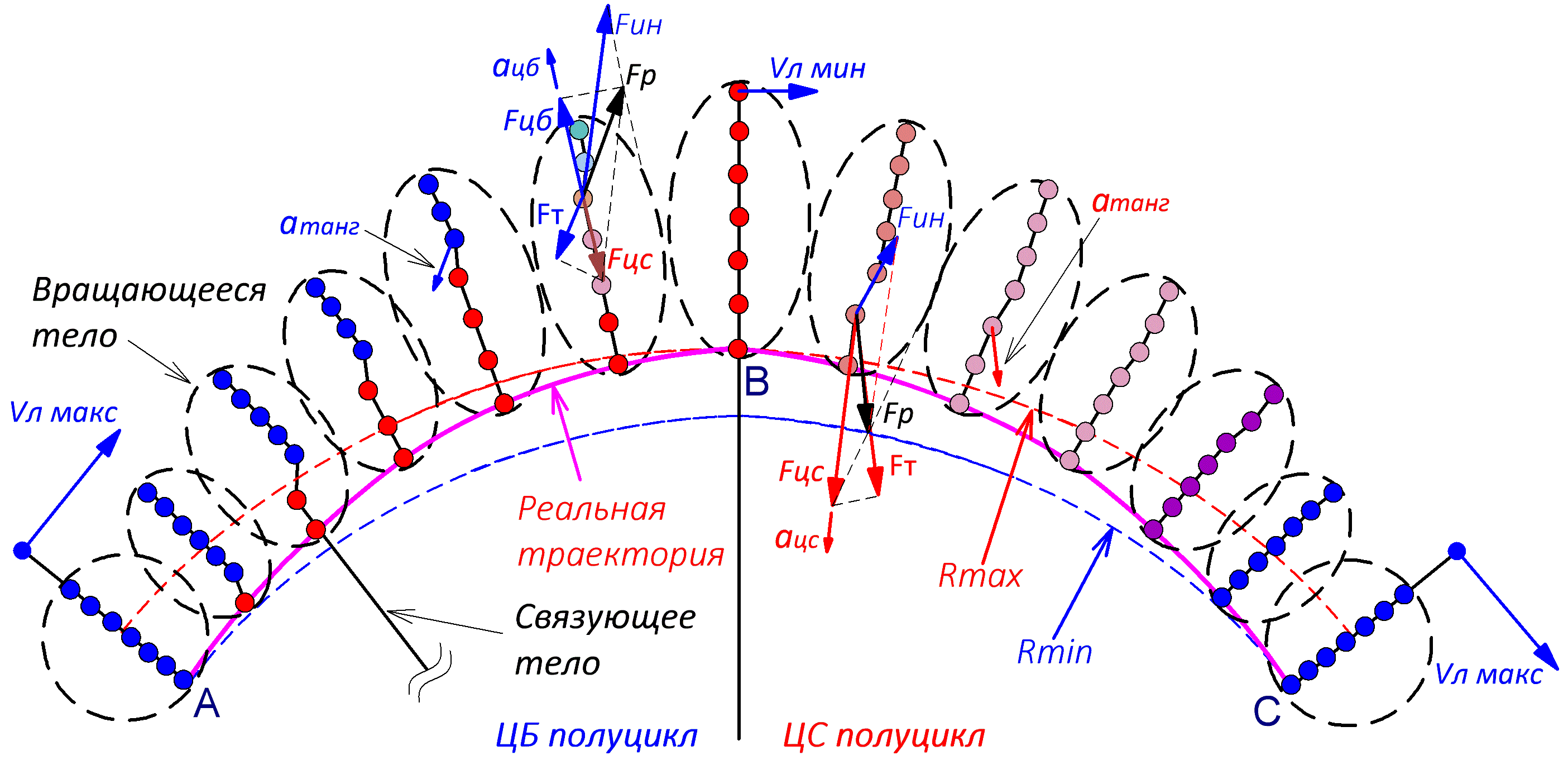
Рис. 3.2.2 Движение тела от центра вращения в радиальном направлении происходит в условиях нарастающего противодействия силы упругости, что приводит к общему замедлению линейного движения. Однако за счет увеличения угла изгиба (ψ) проекция линейной скорости на радиальное направление некоторое время увеличивается, что обеспечивает опережающий прирост силы инерции в радиальном направлении и соответственно ускоренное радиальное движение тела от центра вращения. Представив структуру вращающегося тела в виде совокупности элементарных масс, связанных между собой упругими связями, мы можем наглядно проиллюстрировать механизм инерции поэлементной поддержки (см. Рис. 3.2.3). При этом тот факт, что элементы тела реально взаимодействуют между собой, снимает все вопросы относительно реальности сил инерции поэлементной поддержки в принципе и центробежной силы вращательного движения в частности.
Рис. 3.2.3 В точке (А) центробежная и центростремительная сила, а также тангенциальные силы уравновешивают друг друга. При этом все элементы тела какое–то мгновение движутся по инерции. Первым теряет инерционное движение самый ближний к связующему телу элемент тела. Связующее тело тянет его к центру вращения, в то время как внешние элементы тела по инерции удаляются от центра вращения. Конечно же о движении по инерции здесь можно говорить лишь условно, т.к. взаимодействие распространяется по вращающемуся телу достаточно быстро и не равномерно. Тем не менее, в некотором приближении условно академически можно считать такое движение инерционным. При этом между первым захваченным элементом и удаляющимися от центра элементами образуется вполне реальное общее центробежно–центростремительное напряжение. Классическая физика разделяет это напряжение на две векторные силы. Внешний вектор этого напряжения и есть абстрактная классическая центробежная сила, а внутренний вектор обозначает абстрактную центростремительную силу (см. гл. 3.1.). Поскольку все элементы, как самого вращающегося тела, так и связующего тела сами являются равноправными вращающимися телами, то разделение на вращающееся тело и на связующее тело весьма условно. Поэтому для простоты условно - академически будем считать связующее тело некой гипотетической нематериальной упругой субстанцией. Тогда на связующее тело однозначно действует одна только центробежная сила ЦБС, а на ЦМ вращающегося тела – центростремительная сила упругости связующего тела ЦСС. Однако в отличие от нашего условно нематериального и без элементного абстрактного связующего тела вращающееся тело состоит из множества массовых элементов, между которыми возникает точно такое же центробежно–центростремительное напряжение, как и между всем вращающимся телом и связующим телом. Следовательно, на все элементы тела, а значит и на всё тело в целом действует не только ЦСС, но и вполне обычная ЦБС инерции поэлементной поддержки. Как только первый же элемент тела оказывается захваченным связующим телом (присоединённым к связующему телу), на него со стороны ещё не присоединённых элементов тут же начинает действовать вполне реальная ЦБС. А на каждый внешний элемент тела соответственно действует ЦСС. До тех пор пока инерционная составляющая движения ещё не присоединённых элементов тела преобладает над центростремительной силой, они будут удаляться от центра вращения, создавая вполне реальную, а вовсе не фиктивную центробежную силу и реальное центробежное ускорение ЦБУ для ранее присоединённой части тела. Из механизма инерции поэлементной поддержки следует, что момент центробежной силы инерции поэлементной поддержки приложен к задним элементам тела, расположенным со стороны центра вращения и останавливаемым в первую очередь. Это означает, что поворот вектора осуществляется относительно его стрелки, как центра вращения. Соответственно разностный вектор, а значит и центробежное ускорение направлены во внешнюю сторону от центра вращения (см. гл. 3.1, Рис. 3.1.4, отдельный фрагмент зелёного цвета). В середине цикла в точке (В) все силы полностью уравновешиваются (Рис. 3.2.3). При этом тело какое–то время вновь движется по инерции, а вектор его скорости направлен по касательной к окружности, как это было в точке (A) в момент захвата тела связующим телом. Однако абсолютная величина вектора скорости тела в этот момент минимальная, т.к. часть его первоначальной энергии перешла в дополнительную по сравнению с остаточной деформацией энергию дополнительного упругого удлинения связующего тела. Это и есть тот момент, когда инерционная составляющая ЦБС становится меньше ЦСС. Начинается второй полуцикл разрядки деформации. Во втором полуцикле центростремительная сила, действует в попутном направлении с инерционным движением тела, сообщая ему центростремительное ускорение. При этом окружная скорость и соответственно центробежная сила растут. В точке (С), аналогичной точке А, все силы на короткое время вновь полностью уравновешиваются, после чего начинается новый цикл механизма образования вращательного движения. Однако линейная скорость тела в точке (С) полностью не восстанавливается до величины, которая была до захвата тела в точке (А), т.к. часть его кинетической энергии сохраняется в остаточной деформации, что будет подробнее показано ниже. В установившемся вращательном движении скорость в точках, аналогичных точкам А и С, восстанавливается только до максимальной скорости установившегося вращения. Казалось бы, из цепочки описанного выше механизма инерции поэлементной поддержки выпадает последний присоединяемый элемент вращающегося тела, к которому уже не может быть приложена центробежная сила поэлементной поддержки, в виду отсутствия за ним других внешних элементов тела. Однако никаких парадоксов и противоречий в этом нет. Как отмечалось выше, в этот момент наступает короткое равновесие всех сил. Поэтому в точке равновесия (В) на последний элемент тела, впрочем, как и на всё тело в целом, не действует не только центробежная, но и центростремительная сила. А вообще общее напряжение всегда перераспределяется между всеми взаимодействующими телами и их элементами, что эквивалентно силовому воздействию на внутренние элементы тела даже тех его элементов, за которыми тело заканчивается. На (Рис. 3.2.3) в ЦБ полуцикле показаны силы, действующие на вновь присоединяемый элемент. Как видно сила инерции поэлементной поддержки (Fин) в сумме с центростремительной силой упругости (Fцс) образуют результирующую силу (Fр). Её проекция на радиальное направление и есть ЦБ сила (Fцб). Поскольку результирующая сила направлена по касательной к спирали, то ЦСС имеет на её направление отрицательную тангенциальную проекцию (Fт). При этом реальное тангенциальное ускорение в ЦБ полуцикле (ат) направлено против линейной скорости. В ЦС полуцикле результирующая сила образуется из тех же силы инерции поэлементной поддержки и центростремительной силы (ЦСС) упругости с той лишь разницей, что теперь преобладает ЦСС. Принципы построения сил полностью аналогичны их построению в ЦБ полуцикле. Некоторые наши оппоненты, сторонники классической физики утверждают, что как только мы присоединили очередной элемент тела к связующему телу, его следует рассматривать как элемент связующего тела. Поэтому с точки зрения классической физики центробежная сила действует не на вращающееся тело, а на связующее тело. Однако поскольку, как мы отмечали выше, связующее тело также фактически является вращающимся телом, то этому утверждению с такими же основаниями можно придать и обратную направленность. При этом либо исчезает вращающееся тело, полностью присоединившись к связующему телу в классической версии, либо связующее тело в нашей версии, что ближе к реальности, т.к. в реальной действительности есть только одно единое вращающееся тело, а роль связующего тела выполняют его внутренние упругие связи. Существует множество реально наблюдаемых фактов, подтверждающих реальность центробежной силы и центробежного ускорения. Например, вращение в вертикальной плоскости ведра с водой, которая не выливается при прохождении верхней точки круговой траектории, несмотря на фиктивность центробежной силы. Фиктивная, т.е. не существующая сила не может противостоять вполне реальной силе тяготения, действующей, в том числе и на воду, а не только на связующее ведро. Поэтому вода и не выливается. Следовательно, реальная центробежная сила проявляется и на уровне самого вращающегося тела–воды. Если по логике классической физики каждый массовый элемент воды при присоединении к связующему телу становится элементом связующего тела, то центробежная сила для воды естественно становится вполне реальной силой. Однако жидкая вода по вполне понятным причинам просто физически не может связывать сама себя и, тем более, ещё что–либо с центром вращения, т.е. не может быть связующим телом! Следовательно есть только одно единое сложное вращающееся тело из воды и ведра, внутренние упругие связи которого выполняют роль связующего тела, что разрешает этот парадокс. Еще более наглядно несостоятельность классической модели вращательного движения проявляется в небесной механике, в которой с точки зрения классической физики, не признающей мировую материальную среду – эфир, связующее тело как бы и вовсе отсутствует в материальном мире. Поэтому вращающееся небесное тело при присоединении к связующему телу должно попросту исчезнуть, как таковое, превратившись в несуществующий эфир или пусть даже во вполне материальное и признаваемое классической физикой поле тяготения, связывающее небесные тела! Но вернёмся к реальному механизму вращательного движения. Итак, на этапе накопления деформации в фазах с первой по третью во вращающейся системе за счет инерции первоначального прямолинейного движения тела проявляется вполне реальное центробежное ускорение, в том числе и по отношению к самому телу. Однако по мере уменьшения радиальной скорости и угла (ψ) уменьшается также разница расстояний (А) и (С), что приводит к уменьшению изгибающего момента. С наступлением равновесия в фазе III (Рис. 3.2.1) или в точке (В) – (Рис. 3.2.3) процесс накопления деформации заканчивается. При этом сила упругости достигает своего максимального значения при минимальной силе инерции линейного движения тела. На этом фоне резко возрастает разгибающий момент, который запускает общую разрядку деформации. Начинается обратный процесс, обеспечивающий ускоренное движение тела, как в тангенциальном, так и в радиальном направлении к центру вращения. В пятой фазе сила инерции вновь приобретает максимальное значение, в то время как сила упругости вновь становиться минимальной. На этом полный цикл преобразования движения по направлению заканчивается, после чего весь процесс повторяется уже в новой точке окружности. Таким образом, центробежная и центростремительная сила, вызывающие соответствующие ускорения, это радиальные составляющие результирующей силы, являющейся геометрической суммой силы инерции и силы упругости, проявляющихся в период накопления и в период разрядки деформации. Как мы уже отмечали, механизм вращательного движения аналогичен механизму отражения. Накопление упругой деформации происходит на разных направлениях в соответствии с разным угловым положением и изгибом связующего тела. Соответственно высвобождение силы упругости накопленной деформации, спровоцированное разгибающим моментом, происходит в обратной последовательности. Таким образом, накопленная деформация обеспечивает эффект «веера отражений» во множестве направлений.
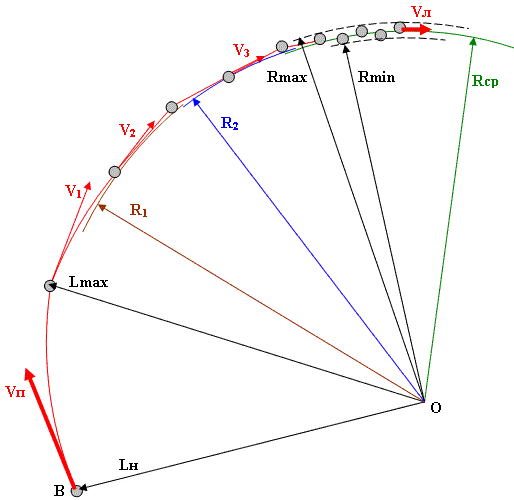
Образование установившегося вращательного движения во многом определяется жесткостью связующего тела, которая зависит от его напряжённости, определяющейся скоростью захвата (Vп). Если скорость (Vп) и соответственно напряжённость недостаточны, то при радиальном удалении тела от центра вращения преобладает растянутая деформация связующего тела при малой изгибной деформации. В отсутствие необходимой изгибной деформации большая часть инерции первоначального прямолинейного движения оказывается скомпенсированной за счёт силы упругости растянутой деформации. При этом скорость движения значительно уменьшается. При определенной линейной скорости и коэффициенте упругости связующего тела, оно может вообще не приобрести необходимую для образования изгибной деформации жесткость. В этом случае на некотором удлинении связующего тела инерция движения окажется полностью скомпенсированной. Вся кинетическая энергия тела перейдет в потенциальную энергию растянутой деформации, а тело полностью остановится. При этом вместо движения по окружности начнутся беспорядочные колебания тела относительно неподвижного центра по непредсказуемой траектории. Таким образом, равномерное движение по окружности может осуществляться только при достаточной жесткости связующего тела, которая за счет изгибной деформации обеспечивает поворот тела в сторону центра вращения с минимальными потерями кинетической энергии линейного движения. При этом напряжённость связующего тела определяется его механическими свойствами и растягивающей центробежной силой инерции, обеспечивающей необходимое напряженно деформированное состояние связующего тела. На начальном этапе образования вращательного движения (см. Рис. 3.2.4) связующее тело удлиняется от недеформированного состояния с начальной длиной (Lн) до максимального удлинения (Lmax), соответствующего максимальной деформации связующего тела. При этом связующее тело приобретает дополнительную жесткость. Следовательно, каждый последующий поворот тела в сторону центра вращения происходит с меньшими потерями тангенциальной скорости и соответственно на меньшем удлинении радиуса.
Рис. 3.2.4 В установившемся вращательном движении минимальное и максимальное удлинение связующего тела приобретают некоторые оптимальные для сложившихся параметров вращения постоянные значения (Rmin) и (Rmax), а тело движется вокруг центра вращения с постоянным средним радиусом и постоянной средней линейной скоростью (Vл). При этом минимальный радиус установившегося вращательного движения (Rmin) определяется некоторой постоянной составляющей остаточной деформации связующего тела, которая обеспечивает ему необходимую для осуществления вращательного движения с соответствующими параметрами жесткость. Таким образом, часть кинетической энергии движения тела с первоначальной скоростью (Vп) переходит в потенциальную энергию остаточной деформации связующего тела, обеспечивая ему оптимальную жесткость. Поэтому первоначально накопленная деформация связующего тела разряжается не полностью, а средняя линейная скорость вращательного движения всегда меньше первоначальной скорости прямолинейного движения (Vп). На рисунке (3.2.4) упрощенно показаны только три фазы установления радиуса вращательного движения (Lmax, R1 и R2), после которых сразу же показано установившееся вращательное движение со средним радиусом (Rср). В реальной действительности переходной процесс может содержать значительно большее количество промежуточных переходных циклов, однако их достаточно сложно изобразить графически в смешанном масштабе. Поэтому мы показали только принципиальную схему установления вращательного движения. Таким образом, вращательное движение представляет собой колебательное движение (см. Рис. 3.2.5), в котором вращающееся тело совершает колебания, как в тангенциальном, так и в радиальном направлении, а величина линейной скорости изменяется по гармоническому закону. Причем на начальном этапе образования вращательного движения размах колебаний может достигать достаточно большой величины, которая может обнаруживаться даже на макроуровне. На рисунке показаны только радиальные колебания в виде колебаний радиуса. Тангенциальные же колебания в статике изобразить не возможно.
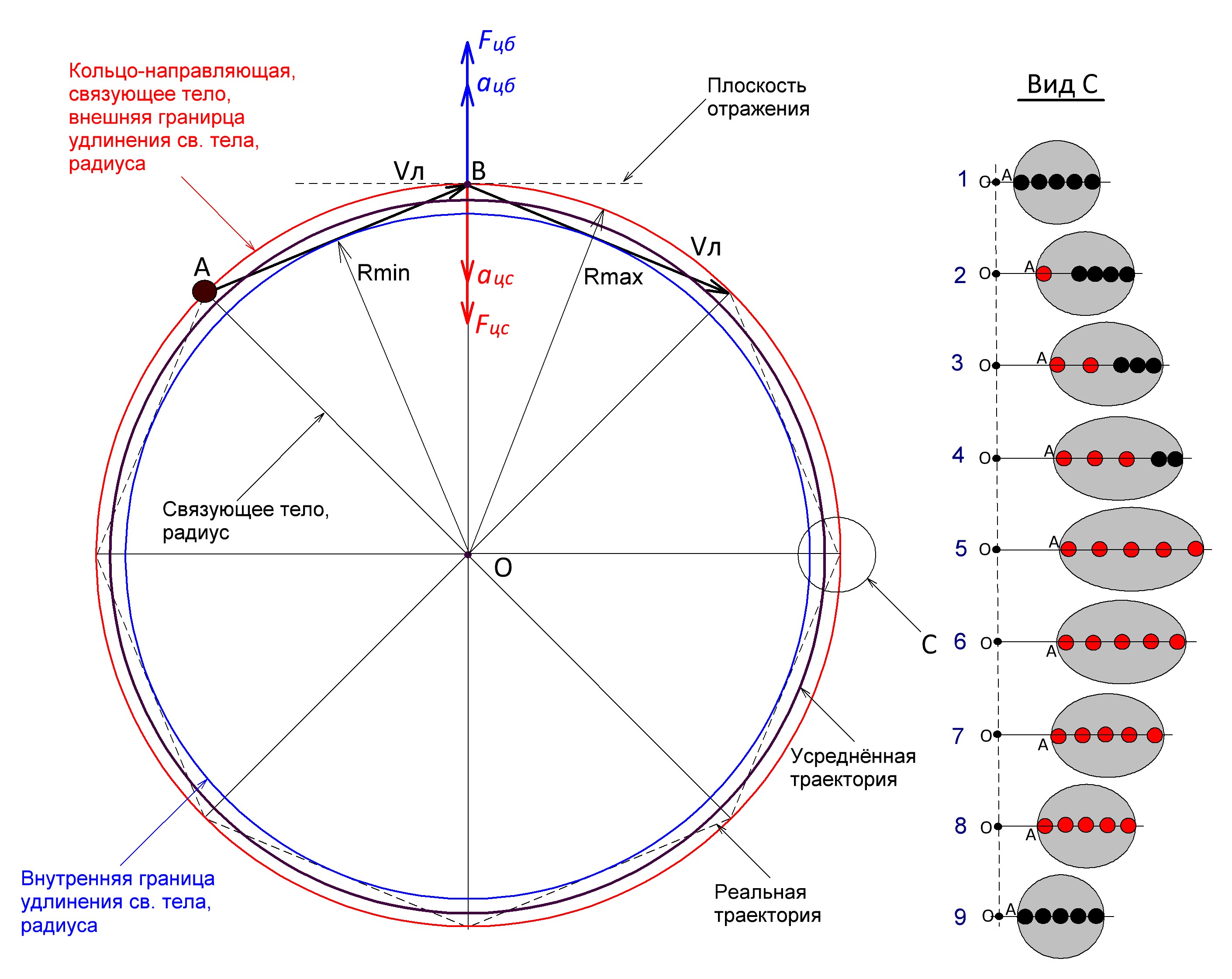
Рис. 3.2.5 На виде С поз. 1 – 5 показано ЦБ ускорение. Поз. 1 – это точка равновесия. В поз. 2 происходит захват св. телом вращающегося тела за его крайний левый элемент. При этом если в первый момент времени ЦБ сила приложена к связующему телу-радиусу ОА, то во всех остальных поз. 2, 3, 4, 5 ЦБ силу и ЦБ ускорение испытывают уже непосредственно и в первую очередь элементы самого тела. А уже через них усилие передаётся связующему телу. После установления равномерного вращения амплитуда колебаний уменьшается, а их частота увеличивается. Поэтому на макроуровне колебательный процесс преобразования движения по направлению не обнаруживается, а все параметры равномерного вращательного движения имеют некоторые усредненные значения. При этом среднее геометрическое ускорение вращательного движения на макроуровне в соответствии с его общей кинематикой должно быть равно нулю не только в тангенциальном, но и в радиальном направлении. Сторонники классической модели вращательного движения считают колебания на начальном этапе образования вращательного движения побочным явлением, которое в установившемся вращении якобы полностью отсутствует. Однако это откровенная глупость, т.к. в этих колебаниях проявляется физический механизм преобразования движения по направлению, без которого не может никакого вращательного движения!Ё! | |
| Просмотров: 2240 | |
| Всего комментариев: 0 | |