| Главная » Статьи » Физика и математика » Мои статьи |
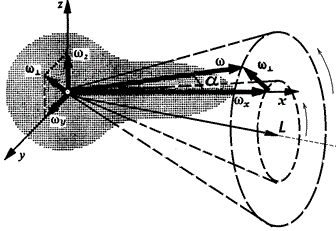
Мы попытались представить нутационное вращение Эйлера более наглядно и дополнили рисунок Матвеева (в оригинале Рис. 113, стр. 321) конусами вращения по описанию Матвеева, которые на его рисунке не обозначены (см. Рис. 4.7.1.3). Очень трудно в соответствии с определением вращательного движения образно увидеть одновременное существование сразу 4-х вращений одного и того же тела, которые следуют из приведенного решения. Их не видит собственно и сам автор, он говорит только о вращении треугольника, состоящего из сторон (ω, ωx, и ω┴). Но то, что вращается относительно сторон этого треугольника из уравнений Эйлера определить невозможно, что подтверждает их физическую несостоятельность. Вместо вращения масс тела относительно осей координат в уравнениях Эйлера фактически вращаются сами вектора угловых скоростей, которые определяются вдоль этих осей через проекции вектора (L), в том числе и вектор угловой скорости полного вращения (см. Рис. 4.7.1.3). А вот угловой скорости вдоль главного, полного, а значит в конечном итоге и единственного суммарного момента импульса, определяющего в динамике вращательного движения реальное суммарное вращение всех масс тела, у Эйлера собственно и нет! Полная угловая скорость (ω = j * ω1 + ω┴) проходит у Эйлера в точном соответствии с векторной геометрией, но в абсолютно необъяснимом для вращательного движения месте тела. Это ещё один абсурд классической динамики вращения твёрдого тела. Таким образом, уравнения Эйлера, в которых по какому-то недоразумению классической физики в единое целое соединены одноимённые понятия, но принадлежащие динамике разных вращательных движений, и осуществлена подмена понятий динамики Ньютона, не отражают реальное вращательное движение твёрдого тела. Общей динамики разных вращательных движений определяющихся разными радиусами и разными плоскостями вращения не может быть в принципе. Далее Матвеев пишет (выделено жирным шрифтом), что тело может вращаться без нутаций, при этом его угловая скорость направлена строго по оси симметрии. Остаётся добавить, что это единственно возможное вращение свободного тела. И наоборот, если есть нутации, т.е. если угловая скорость, ось симметрии и момент импульса не совпадают, то такое движение не свободное (как минимум оно неустановившееся). Но угловые скорости нутации были получены из уравнений Эйлера в предположении, что тело, изображённое на (Рис. 4.7.1.3) вращается в отсутствие внешних сил, а значит и моментов, т.к. в приведённом выводе моменты в уравнениях Эйлера приравнены к нулю. Это означает, что тело должно вращаться свободно. Однако сами нутации свидетельствуют о несвободном движении тела. Закреплённый конец тела просто обязан порождать внешние силы, т.к. это внешнее закрепление. Таким образом, решая уравнения для свободного тела, классическая физика в конечном итоге получила несвободное тело и нутации! Это так же одно из многочисленных противоречий классической динамики вращательного движения. Из решений уравнений Эйлера следует, что нутация - это движение оси симметрии вращающегося тела вокруг неподвижного в пространстве вектора полного момента импульса. Однако, как следует из приведённого выше описания физического механизма образования прецессии и опытных данных движения гироскопа классический полный момент импульса гироскопа не может оставаться неподвижным. Основной момент импульса такого тела прецессирует вместе с телом. Причём в колебаниях относительно средней линии прецессии участвует не только геометрическая ось симметрии (фигуры) гироскопа, но и его основной момент импульса. А поскольку основной момент импульса гироскопа значительно больше момента импульса его прецессии, то по классическим понятиям, допускающим векторное сложение моментов, вместе с основным моментом практически где-то рядом с ним путешествует и полный момент импульса. Таким образом, классическая теория динамики вращательного движения твёрдого тела расходится с реальной действительностью, т.к. она не учитывает реальные силы образования нового вращения, в том числе и силы Кориолиса-Кеплера. Да и вообще она не подается никакой нормальной логике! Движение, изображённое на рисунке (4.7.1.3) больше похоже не на колебания нутации, как циклов прецессии, а на саму прецессию. Но и это не так. Прецессия гироскопа по классическим же представлениям предполагает вращение основного момента импульса по траектории прецессии, а у Эйлера на рисунке (4.7.1.3) циклы прецессии - нутации есть, а самой прецессии нет. Причём и момент импульса собственного (основного) вращения никуда не вращается, т.к. это не вопрос динамики вращательного движения. Момент импульса основного вращения только показывает готовое основное вращение гироскопа, которое устанавливается в каждом цикле прецессии - нутации. Поэтому классическая физика отмечает эту «телепортацию», как отсутствие инерционности прецессии. Тем не менее, вращение на рисунке (4.7.1.3) не соответствует и классическим представлениям о прецессии. Уравнения же Эйлера в общем случае не могут отражать реальную динамику вращения твёрдого тела, особенно если тело сложной пространственной конфигурации, т.е. несимметричное. В таком движении по мгновенным значениям моментов импульса обратно-криволинейного движения очень сложно определить траекторию его полного момента. Математика рождена физикой. Поэтому физические корни математики иногда в некоторых частных случаях дают правильный результат даже при её бездумном применении (см. Рис. 4.7.1.1). Но в сложных случаях уравнения Эйлера вряд ли имеют физически правильные решения, т.к. в этих случаях движение твёрдого тела больше соответствует произвольному криволинейному движению его отдельных частей, которое динамикой вращательного движения не определяется. С этой задачей справится только динамика Ньютона. Единственным случаем, в котором переходный процесс практически не вносит заметных искажений в динамику вращательного движения разных вращений на макроуровне, является гироскоп. Отличительной особенностью движения гироскопа является его очень быстрое вращение относительно главной оси симметрии и в связи с этим большая величина его кинетической энергии. При этом для сравнительно малых внешних воздействий процесс преобразования основного движения в новое вращение и разрушение основного вращения значительно растягивается во времени, а переходный процесс практически переходит на микроуровень. Это позволяет в некотором приближении рассматривать прецессию и основное вращение гироскопа в своих плоскостях в рамках динамики вращательного движения с постоянным радиусом, но только каждое в отдельности. Это так же некое подобие квантования единого Ньютоновского процесса на разные вращения. | |
| Просмотров: 1046 | |
| Всего комментариев: 0 | |