| Главная » Статьи » Физика и математика » Мои статьи |
Теперь перейдём к графической иллюстрации всего сказанного в настоящей главе на примере абсолютной траектории поворотного движения с постоянной скоростью радиального относительного движения. (см. Рис. 7.3.3).
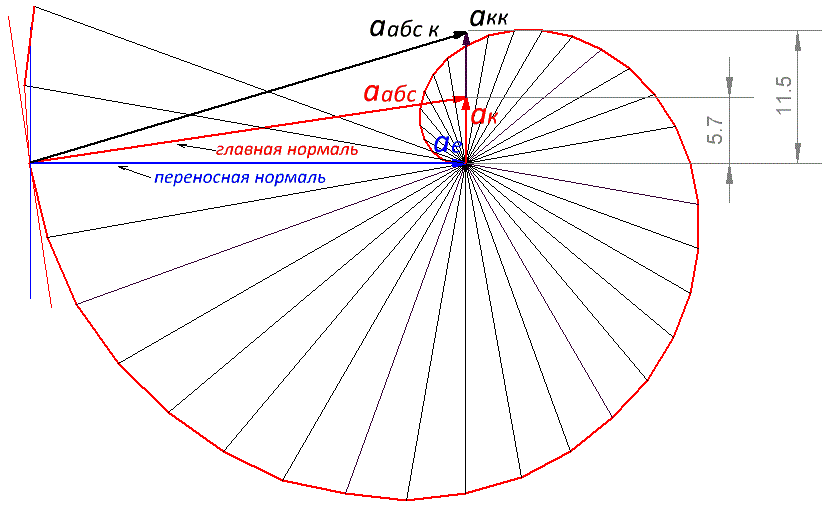
Рис. 7.3.3 Исходные данные: ω = 1; Rнач = Δφ = 100 – дискретность поворота радиуса (для построения приемлемо плавной спирали); ΔR = 1 м Расчётные данные: ΔRу = ΔR * 3600 / Δφ = 36 м – удлинение радиуса за один оборот: (необходимо для определения радиальной скорости); t = 2π/ω = 6,28 с (т.к. радиальное движение у нас длится один полный оборот) Rконечный = Rнач + ΔRу = 37 м; Vr = ΔRу / t = 5,73 м/с; ае = ω2 * R = 37 м /с2; ак = ω * Vr = 5,73 м /с2; акк = 2 * ω * Vr = 11,5 м /с2 Численные значения и пространственная ориентация абсолютного ускорения в нашей версии (аабс) и абсолютного ускорения классического по теореме Кориолиса (аабс к) по формулам не рассчитывались. Вектора этих ускорений получены графически при геометрическом сложении рассчитанных значений переносного ускорения (ае), ускорения Кориолиса в нашей версии (ак), и классического ускорения Кориолиса (акк). Их численные значения это лишь следствие из полученных графических построений в соответствии с векторной геометрией на основе исходных и расчетных данных. Как видно из рисунка, абсолютное ускорение криволинейного движения по теореме Кориолиса с учётом ускорения Кориолиса в нашей версии соответствует и нашей версии абсолютного ускорения, как центростремительного ускорения криволинейного движения, направленного вдоль главной нормали. Классическая версия абсолютного ускорения криволинейного движения противоречит классической же теореме Кориолиса. На рисунке (7.3.3) видно, что классическое абсолютное ускорение (аабс.к) состоит из нормального ускорения (аабс), которое уже представляет собой абсолютное ускорение в нашей версии, и тангенциального ускорения в виде ещё одной половины классического ускорения Кориолиса, не соответствующей полному ускорению точки. Складывая нормальное ускорение с половиной классического ускорения Кориолиса, классическая физика фактически учитывает реальное ускорение Кориолиса дважды.
| |
| Просмотров: 1672 | |
| Всего комментариев: 0 | |