| Главная » Статьи » Физика и математика » Мои статьи |
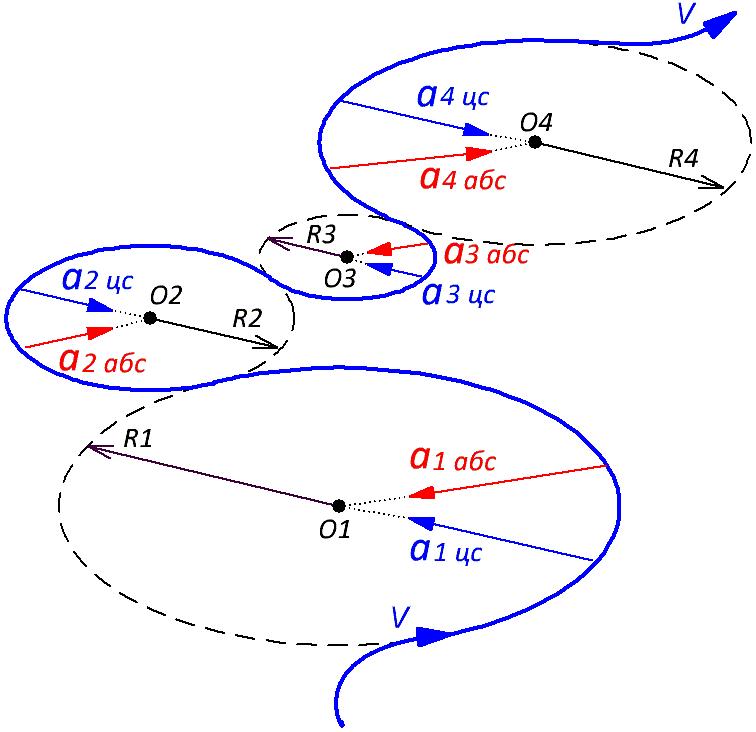
Абсолютное ускорение произвольного движения. Поскольку любое измерение чего-либо занимает определённое не нулевое время, то со 100% точностью можно измерить только установившиеся или постоянные во времени, они же мгновенные, параметры переменных процессов, изменяющихся по неизвестному закону. Это в частности справедливо и для переменного движения, изменяющегося по неизвестному закону. При этом установившимися или постоянными параметрами характеризуется только равномерные процессы и равномерные движения. Таким образом, в точке могут быть определены мгновенные параметры только установившегося равномерного движения. Для произвольного движения мгновенные параметры могут быть определены только, как усреднённые постоянные параметры на участке траектории не нулевой длины. Это и есть академическая «точка» для произвольного движения, изменяющегося по неизвестному закону. При этом, поскольку для достижения одинаковых динамических параметров в прямолинейном и в криволинейном движении требуются разные затраты, то следует различать и разные академические «точки» для прямолинейного и криволинейного движения. Очевидно, что параметры прямолинейного неравномерного движения могут быть измерены, как усреднённые параметры равноускоренного прямолинейного движения в усреднённой «прямолинейной точке». Что касается произвольного криволинейного движения, то с любым его участком всегда можно сопоставить дугу окружности равномерного вращательного движения, геометрические, динамические и кинематические параметры которого будут мало, чем отличаться от усреднённых параметров соответствующего участка криволинейной траектории. Центростремительное ускорение этого вписанного равномерного вращательного движения будет достоверно отражать усреднённое ускорение реального движения на этом участке (см. Рис. 7.3.1). Вопрос только в точности этого сопоставления, который легко решается с уменьшением величины сопоставляемых участков.
Рис. 7.3.1
Таким образом, измерительным эталоном (измерительным калибром) «мгновенного» абсолютного ускорения произвольного криволинейного движения является центростремительное ускорение равномерного вращательного движения по вписанной в траекторию криволинейного движения окружности. В классической физике абсолютное ускорение произвольного криволинейного движения определяется двумя способами. По теореме о полном ускорении точки на траектории (далее: теорема о проекции ускорения) или по теореме Кориолиса о сложении ускорений. Однако эти две теоремы физически противоречат, как здравому смыслу, так и друг другу. Рассмотрим подробнее эти противоречия. Начнём с теоремы «О равенстве скорости соответственной точки годографа полному ускорению точки», которая используется для доказательства теоремы о проекции ускорения (см. Жуковский Н. Е. «Теоретическая механика», издание второе, ГОСУДАРСТВЕННОЕ ИЗДАНИЕ ТЕХНИКО–ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ, МОСКВА–ЛЕНИНГРАД,
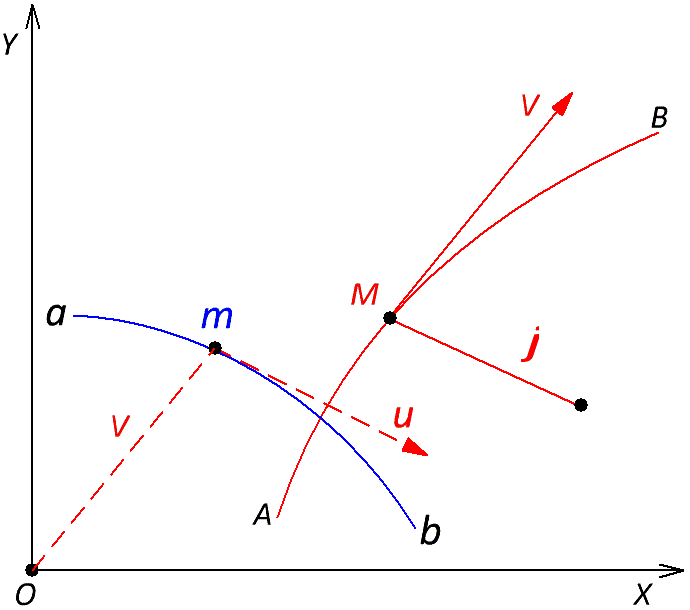
Фиг. 22
Пусть уравнения точки М имеют вид (х = f(t), y = g(t)). Тогда координаты точки (m) или равного ему геометрически вектора скорости (V) равны (х’ = f’(t) = dx / dt, y’ = g’ (t) = dy / dt). При этом проекции вектора (u), который является скоростью точки (m), равны (d2x / dt2, d2y / dt2), что соответствует координатам проекции полного ускорения (j). Следовательно, геометрически равны и сами векторы (u = j). Вот только нет никаких гарантий, что вторая производная скорости произвольного криволинейного движения соответствует реальному приращению именно ускоренного движения, в котором отсутствуют участки, пройденные за счёт постоянной составляющей скорости движения. Это может быть гарантированно только в равномерном вращательном движении. Теперь рассмотрим саму теорему о проекции ускорения: «Проекция полного ускорения на тангенциальное направление равна производной от величины скорости по времени, а проекция полного ускорения на главную нормаль к траектории равна квадрату скорости, делённому на радиус кривизны траектории данной точки» (см. Жуковский Н. Е. «Теоретическая механика», издание второе, ГОСУДАРСТВЕННОЕ ИЗДАНИЕ ТЕХНИКО–ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ, МОСКВА–ЛЕНИНГРАД,
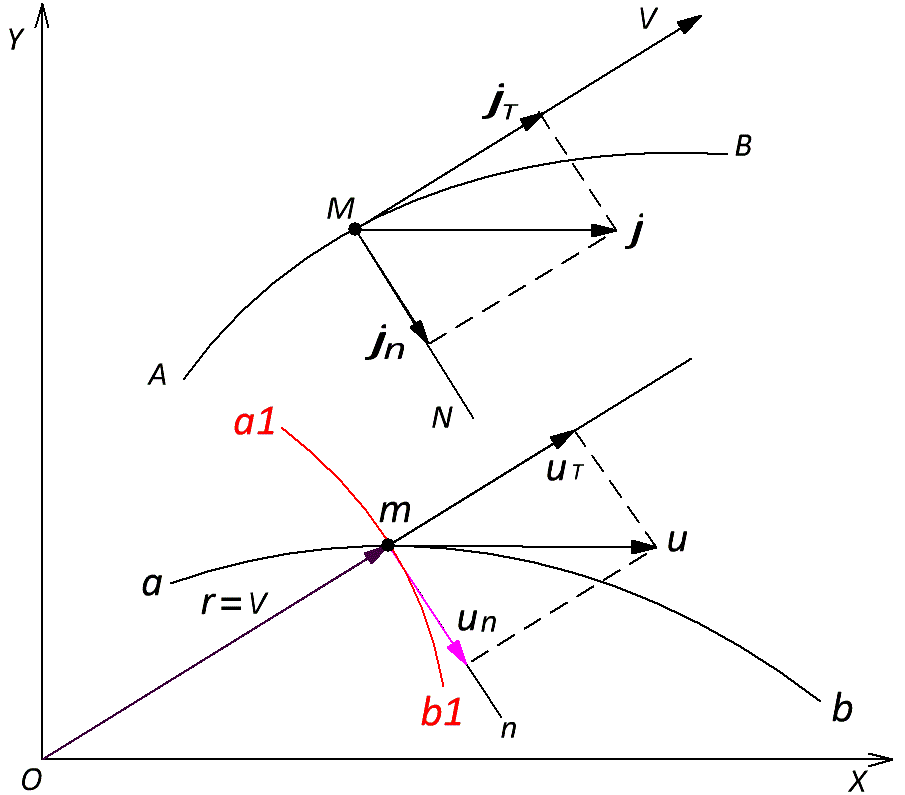
Фиг. 25 В первой части теоремы определяется тангенциальная составляющая, которая равна: jt = uТ = dr / dt = dV / dt Для определения проекции полного ускорения на главную нормаль Жуковский ссылается на известный из анализа факт, что отношение угла смежности (dφ) к бесконечно малой дуге (dS), на которую опирается этот угол, есть мера кривизны дуги в этой точке (dφ / dS = 1/R). При этом нормальное ускорение по Жуковскому равно: jn = r * ω = r * dφ / dt = V * dφ / dt Умножив и разделив правую часть на (dS) Жуковский получает проекцию полного ускорения на главную нормаль в виде центростремительного ускорения вдоль главной нормали: jn = V * (dφ / dS) * (dS / dt) = V * (1 / r) * V = V2 * 1 / r = V2 / R Что и требовалось доказать. Однако при внимательном рассмотрении это доказательство не состоятельно. Радиус кривизны и соответственно сама мера кривизны, которая положена в основу доказательства теоремы, могут быть только постоянными величинами по определению. Действительно, понятие кривизны определяется выражением: dφ / dS = 1 / r где: dφ – некий фиксированный, т.е. постоянный угол смежности dS – фиксированная бесконечно малая дуга, на которую опирается фиксированный угол смежности (dφ) Но, как известно, соотношение двух фиксированных (постоянных) величин так же есть величина постоянная. Следовательно, кривизна, и радиус кривизны могут быть либо постоянными величинами равномерного вращательного движения, либо постоянными усреднёнными параметрами произвольного криволинейного движения в академической «криволинейной точке». Выборочное усреднение параметров в одном и том же интервале времени не возможно в принципе. Либо усредняются все параметры движения и тогда – это «криволинейная точка» с абсолютным обобщённом центростремительным ускорением, либо – это разные точки в разных интервалах времени и соответственно ускорения разных движений, что гарантированно разваливает доказательство теоремы. Совершенно очевидно, что стрелка вектора скорости (r = V), вращающегося с обобщённым центростремительным ускорением в точке (М) рисует вовсе не годограф (ab), а годограф (a1b1). А это есть ни что иное, как годограф абсолютной скорости движения по вписанной в траекторию окружности в точке (М), из которого определяется абсолютное центростремительное ускорение точки, направленное вдоль главной нормали, т.е. (jn = un = j). Таким образом, Жуковский фактически сам показал, что полным ускорением точки является нормальное центростремительное ускорение равномерного вращательного движения, вписанного в траекторию в соответствующей «криволинейной точке». Совершенно очевидно, что центростремительное ускорение, как собственно и само равномерное вращательное движение, может проявляться только в одном случае, когда ни какие другие ускорения и другие движения не будут им в этом мешать. А не мешают центростремительному ускорению и движению с ним только те ускорения, которые оно – центростремительное ускорение в его родной «криволинейной точке» и обобщает, т.е. его собственные составляющие. Отсюда следует, что в усреднённой «криволинейной» точке не может одновременно проявляться нормальное центростремительное ускорение и ускорения, не входящее в его состав, уже обобщающий все возможные ускорения в этой усреднённой «криволинейной» точке. Поскольку обобщённое центростремительное ускорение в классической физике академически приравнивается к обычным физическим ускорениям, то его можно складывать с векторами любых других ускорений. Однако при этом необходимо помнить, что складываются не только ускорения, но и сами движения, которые осуществляются с этими ускорениями. При этом сумма ускорений, начало сложения которых осуществляется в некой точке, окончательно формируется уже не в этой точке, а в новой общей «криволинейной» точке в виде центростремительного ускорения равномерного вращательного движения вписанного в эту точку. При этом усреднённое в криволинейной точке ЦСУ учитывает, в том числе и тангенциальное ускорение, которое сказывается на средней величине скорости усреднённого равномерного вращательного движения. По теореме Кориолиса абсолютное ускорение складывается из полного ускорения относительного движения, полного ускорения переносного движения и ускорения Кориолиса. В случае равенства нулю относительного ускорения, абсолютное ускорение равно сумме переносного ЦСУ вдоль нормали к окружности переносного вращения и ортогонального ему ускорения Кориолиса, что противоречит, как теореме о проекции полного ускорения на тангенциальное направление и на главную нормаль к траектории, так и приведённому выше здравому смыслу. ***
| |
| Просмотров: 2151 | Комментарии: 1 | |
| Всего комментариев: 1 | |
|
| |