| Главная » Статьи » Физика и математика » Мои статьи |
Гравилёт Кашубы В. Ю. В. Ю. Кашуба (Белореченск, Краснодарский край) предлагает антигравитационный инерцоид, изображённый на рисунке (12.4.9). По мнению автора, центробежная сила кольца, вращающегося в плоскости перпендикулярной радиусу Земли, обеспечит инерцоиду антигравитационную силу, направленную против силы тяготения Земли.
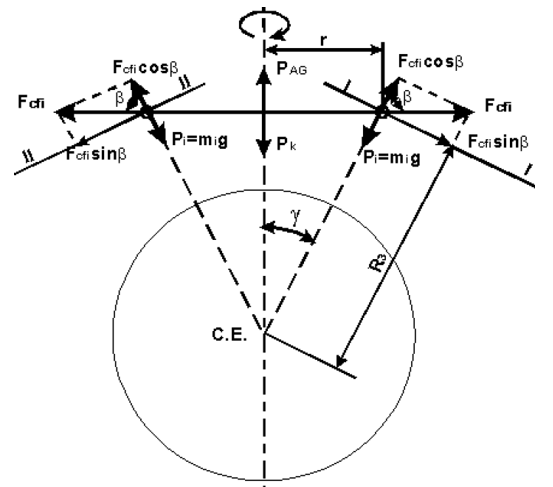
Рис. 12.4.9 Обозначения на рисунке: Fcfi = mi * V2 / r – центробежная сила инерции материальной точки на кольце Pi = mi * g – сила тяжести материальной точки на кольце V – окружная скорость вращения кольца Rз = 6371 км – радиус Земли По замыслу автора для того чтобы материальная точка находилась в невесомости должно выполняться условие: mi * g – Fcfi * cos β = 0 Автор пишет, что если вращение происходит близко к поверхности Земли, то: сos β = sin γ = r / Rз тогда: Fcfi * cos β = mi * (V2 / r) * (r / Rз) = mi * V2 / Rз То есть условие (mi * g – Fcfi * cos β = 0) выполняется при V, равной первой космической: V = V1 = (g * R3)1/2 Как видно, анти гравитационная сила инерцоида Кашубы не зависит от радиуса кольца. Это совершенно естественно, т.к. центробежные силы гироскопа в плоскости кольца диаметрально уравновешиваются, превращаясь во внутреннее статическое напряжение кольца. Естественно, что внешние неуравновешенные силы по отношению к кольцу не могут являться проекциями его внутренних сил. А вот линейная скорость в плоскости кольца ничем не уравновешена. Она является внешней для Земли, не только в плоскости кольца, но и в плоскости орбиты, которая проходит через радиус Земли (Rз) и вектор линейной скорости кольца. При этом равновесие с силой тяготения (mi * g - Fор. = 0) обеспечивает именно орбитальная центробежная сила (Fор. = mi * V2 / Rз), а вовсе не внутренняя центробежная сила кольца (Fcfi = mi * V2 /r) в виде своей формальной проекции (Fcfi * cos β). Именно в этом и заключается физический смысл вращательного движения в небесной механике, который никак не связан с внутренними силами гироскопа. Однако даже если для отдельной материальной точки кольца центробежные силы теоретически и уравновешивают силу тяготения при первой космической скорости, то практически не только для всего гироскопа в целом, но и для отдельных точек кольца, никакой невесомости не наступит. Механизм формирования вращательного движения в связанном вращении, каковым является система гироскопа, и в небесной механике принципиально идентичны (см. главу 3.4.). Существенно отличаются только абсолютные величины их кинематических и динамических параметров. Если в связанном вращении механизм его формирования осуществляется на микроуровне, то в небесной механике он выходит на макроуровень. Грубый оценочный расчёт, приведённый в главе (3.4.) показывает, что длина одного законченного цикла формирования вращательного движения в небесной механике может составлять от 160 метров до 8000 метров. Может быть мы несколько и ошибаемся в своей оценке, но именно с небесными размерами механизма преобразования движения по направлению в небесной механике и должен быть связан размер летающего по законам небесной механики гироскопа, иначе вращательное движение вдоль орбиты просто не сформируется. Однако даже с небесными размерами гироскоп всё равно не полетит, т.к. все элементы диска гироскопа жестко связаны между собой, что не позволит каждой его точке в отдельности соблюдать траекторию механизма вращательного движения вдоль орбиты. В этом смысле весь жесткий диск гироскопа соответствует одной точке, т.е. единому телу с внутренним движением точек, которое в целом вдоль орбиты не движется и соответственно никакие силы, противодействующие тяготению, для гироскопа в целом не образуются. Хотя, на наш взгляд, диаметрально уравновешенные точки, движущиеся по кольцу и имеющие полную свободу действия, кроме диаметральной связи, вполне могли бы уравновесить силу тяготения, двигаясь по своему локальному кольцу, а не по орбите. Однако это уже не гироскоп. Это другое устройство и другая тема. Скажем только, что на практике она, мягко говоря, очень труднореализуемая. В подтверждение своей идеи автор ссылается на данные реальных опытов с гироскопами, в которых зафиксировано небольшое изменение веса. Однако не всё так просто, как кажется на первый взгляд. Реально существующие гироскопы вопреки расчётам автора почему–то упорно не хотят летать, а изменения веса вовсе не соответствуют его расчётам. Приведём простой пример этого несоответствия: Пусть радиус гироскопа – 0,2 м. Линейная скорость орбитального движения вблизи Земли нам известна (V = 7900 м / с). Тогда, для того чтобы такой гироскоп в соответствии с теорией автора полностью потерял вес, его угловая скорость должна быть равна: ω = V / 2* π * r = 7900 / (6,28 * 0,2) = 6290 [об /с] = 377389 [об / мин] Это вполне достижимая для гироскопов скорость вращения, по крайней мере, для экспериментальных гироскопов. Однако ни один земной гироскоп ещё не полетел и даже не завис над лабораторным столом. А изменение веса гироскопа при их свободном падении, настолько мало, что его трудно даже зафиксировать. При этом экспериментаторы объясняют изменение веса вовсе не центробежной силой в плоскости кольца гироскопов и даже не центробежной силой относительно Земли, т.е. вовсе не небесной механикой Ньютона, а якобы неизвестным пока физике влиянием поля инерции гироскопа на поле тяготения. Но это уже другой вопрос. Подробнее см. А. А. Астахов "Физика движения", глава 3.4; 12.4
| |
| Просмотров: 1251 | |
| Всего комментариев: 0 | |