| Главная » Статьи » Физика и математика » Мои статьи |
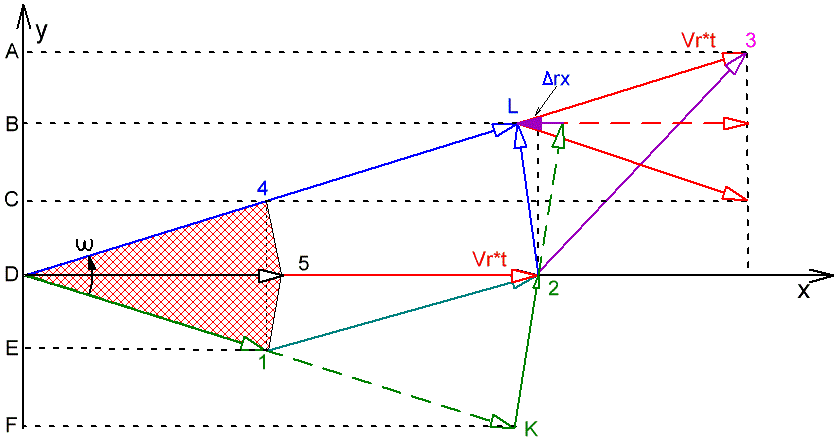
Пресловутая двойка фигурирует и в выводе ЦС ускорения по трёхточечной схеме. Однако это так же, как и в случае с прямолинейным ускоренным движением связано не с удвоением ускорения, а со средней скоростью ускоренного движения. Покажем это на рисунке (4.1.1.3). Приращение пути за счёт ЦСУ равно: ∆rx = (DL - D”2”) - (D”2” - DK) = DL - 2 * D”2” + DK а = (cos(ωt) * (DL + DK) - 2 * D”2”) / t2 Поскольку DL = DK, а угловая скорость (ω) - постоянная, то |DL - D”2”| = |D”2” - DK| DL + DК = 2 * D”2” Тогда: а = (cos(ωt) - 1) * 2 * D”2”) / t2 Как видно, здесь двойка относится вовсе не к удвоению приращения пути за счёт ускорения. Это промежуточный результат связанный с вычислением средней скорости, что становится очевидным при разложении функции (cos(ωt) - 1) в ряд Тейлора: cos(n) - 1 = - 1 = -n2 / 2… Тогда: a = - (((ωt) 2 / 2) * 2 * D”2”) / t2 = ω2 r После сокращения (2) и (t2), получаем a = - = ω2 r, где D”2” = r На рисунке (4.1.1.3) приведена классическая трёхточечная схема применительно к криволинейному движению. Временной интервал между точками (1, 2, 3), если считать по порядку по ходу движения, как и прежде - одна секунда. Очевидно, что если бы не было радиальной скорости, то все три радиуса-вектора (DK), (D “2”), и (DL) были бы одинаковыми. При этом разница проекций (DK) и (DL) на ось (Y) была бы равна нулю (ВD - DF = 0), что означает отсутствие ускорения вдоль тангенциального направления (Y).
Рис. 4.1.1.3 Очевидно, что с учётом радиального движения радиус-вектор (D ”1”) будет короче радиуса-вектора (DK) на (“1” К = Vr * t * sin (ω * t)), а радиус-вектор (D “3”) длиннее радиуса-вектора (DL) на величину (L “3” = Vr * t * sin (ω * t)). А поскольку разность проекций на ось (Y) областей (D “4” “5”) и (D “5” “1”) равна нулю (красная штриховка), то приращение вдоль оси (Y) соответствует двум проекциям приращения радиуса — (AC = АВ + ВС = 2 * Vr * t * sin (ω * t)), или для малых углов (AC = 2 * Vr * ω * t2). Это и есть классическое математическое подтверждение двойки в ускорении Кориолиса. Однако это справедливо только в отсутствие истинной силы Кориолиса-Кеплера. Естественно, что прирост средней скорости даёт и среднее ускорение при вычислении. При этом стопроцентная точность трёхточечной схемы обеспечивается только при равноускоренном движении на всём протяжении обоих смежных участков. В противном случае одинаковое среднее ускорение может быть получено при разных ускорениях на каждом участке с максимальным отличием в два раза, когда приращение координат на одном из участков достигнуто без ускорения, т.е. с нулевым ускорением за счёт неизменной скорости. Поворотное движение это на наш взгляд, как раз то случай. В поворотном движении нет идеального ВД ни вектора тангенциальной скорости, ни вектора радиальной скорости. Радиальное движение делает незавершёнными, как цикл ВД тангенциальной скорости, так и цикл ВД радиальной скорости. При этом, очевидно, поворот вектора радиальной скорости за счёт половины поддерживающей силы осуществляется через механизм отражения, с ускорением которого и осуществляется и приращение тангенциальной скорости по величине. Более подробно о механизме формирования поворотного движения будет изложено в следующей главе (4.1.2.). Как показано выше, если путём компенсации истинной силы Кориолиса-Кеплера поддерживать на неизменном уровне только линейную скорость переносного вращения, то ускорение Кориолиса будет равно нулю. Именно это и происходит в поворотном движении. Однако классическая трёхточечная схема не видит этого обнуления половины ускорения Кориолиса, т.к. в графическом решении не отражается компенсация половины поддерживающей силы за счёт силы Кеплера. В ней есть только общее приращение движения без учёта истинного вклада в него поддерживающей силы. Трёхточечная схема отсекает только начальную скорость от измеряемого участка, исключая тем самым обеспечиваемое начальной скоростью приращение пути без ускорения. Но то, что происходит внутри измеряемого участка не видит ни одна графическая схема. Это можно учесть исключительно только аналитически и условно отобразить графически. А анализ показывает, половина поддерживающей силы тратится на компенсацию силы Кеплера. Это означает, что половину приращения, определяемого по трёхточечной схеме тело проходит без ускорения с постоянной скоростью. Таким образом, полное напряжение Кориолиса в статике действительно соответствует классической силе Кориолиса (Fпк = 2 * m * Vr * ω). Однако динамические ускорение и сила Кориолиса оказываются при этом вдвое меньше классических аналогов (акд = Vr * sin (ω * t) / t = Vr * ω, Fкд = m * Vr * ω). | |
| Просмотров: 67 | |
| Всего комментариев: 0 | |