| Главная » Статьи » Физика и математика » Мои статьи |
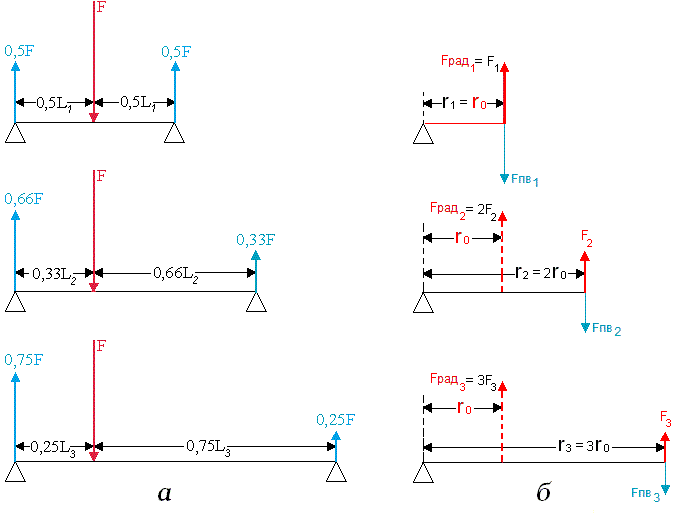
При наличии принципиальной физической аналогии динамики Ньютона с динамикой мерного вращения нет никакой необходимости прятать эту аналогию и в математических символах. Если обозначить угловую скорость и угловое ускорение приведённого вращения символами скорости и ускорения из динамики Ньютона с индексами приведённого вращения (рад), то мы получим не только принципиальную, но и полную внешнюю аналогию. ωрад → Vрад [мрад / с] = ω * r / rрад εрад → арад [мрад / с2] = ε * r / rрад Мерный радиан можно также обозначить как (r0), т.е.: rрад = r0 При этом индексы приведённого вращения (рад) и (0) нужны только для того, чтобы отличать ньютоновскую динамику вращательного от поступательного движения, которые ничем иным, кроме систем отсчёта радиальной для углового перемещения и прямоугольной для поступательного линейного перемещения не различаются. Таким образом, в мерной динамике вращательного движения угловая скорость и угловое ускорение, а также сила и работа по физическому смыслу и по размерности полностью аналогичны соответствующим физическим величинам динамики Ньютона. С введением мерного радиана из физики навсегда исчезнут абсурдные теории вроде классической динамики вращательного движения и алогизмы явления Кориолиса и классической версии ускорения произвольного движения, а также некоторые другие. *** Физика и принцип работы рычага, связанные с обратно пропорциональным распределением сил упругости в зависимости от длины плеч рычага, наглядно показаны на рисунке (3.4.2 а). Чем больше плечо, тем меньше удельная нагрузка на единицу его длины и наоборот. Поэтому на равных плечах образуются одинаковые силы равные половине внешней силы (F). Соответственно при разных плечах соблюдается соотношение (F1 / F2 = r2 / r1), что и есть правило рычага.
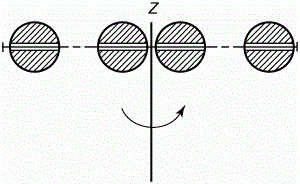
На рисунке (3.4.2 б) приведена геометрическая иллюстрация физического смысла мерной динамики вращательного движения, основанная на правиле рычага. Справа на разных плечах от (r = r0) до (r = 3r0) показаны силы (F1-F3), уравновешивающие противостоящие им силы (Fпв1 – Fпв3) на том же радиусе на котором действуют противостоящие силы. На мерном радиане (r = r0) эти же противостоящие силы могут быть уравновешены приведёнными силами (Fрад1 - Fрад3), но уже с коэффициентом (К = r / rрад) по сравнению с противостоящими им силами на реальном радиусе. Верхняя часть рисунка (3.4.2 б) это непосредственно само мерное вращение, т.е. единая универсальная мера пространства Ньютона в радиальной системе отсчёта вдоль окружного движения. Здесь коэффициент приведения к мерному вращению равен единице (К = r / rо = 1). При этом сила на текущем радиусе, он же мерный радиан, равна силе приведённого вращения (Fрад = F). На средней части рисунка (3.4.2 б) текущий радиан–радиус в два раза больше мерного радиана–радиуса (К = r / rо = 2). Следовательно, приведённая к мерному радиану сила в полном соответствии с уравнением мерной динамики вращательного движения и правилом рычага равна (Fрад2 = 2F2). На нижней части (К = r / rо = 2), соответственно (Fрад3 = 3F3). Практическое применение мерной динамики вращательного движения приведено в главе (4.2.) при выводе формулы силы и ускорения Кориолиса через мерную динамику вращательного движения. *** А теперь обратимся по поводу динамики вращательного движения к известному популяризатору классической физики и нашему традиционному заочному оппоненту, известному нашему читателю по главе 1, доктору физики, профессору Гулиа Н. В. В своей книге «Физика: Парадоксальная механика в вопросах и ответах» он пишет: «Инертность массивной точки (тела) зависит только от ее массы. Масса является мерой инертности тела при поступательном, в том числе и прямолинейном, движении. Значит, при таком движении на инерцию не влияет распределение масс в теле, и это тело можно смело принять за материальную (массивную) точку. Масса этой точки равна массе тела, а расположена точка в центре масс или центре инерции тела. Если же вращать вокруг вертикальной оси Z стержень с насаженными на него массивными грузами (рис. 6), то можно заметить, что пока грузы находятся близ центра, раскрутить стержень (жирный шрифт наш – авт.) легко. Но если грузы раздвинуть, то раскрутить стержень станет труднее, хотя масса его не изменилась.
Рис. 6. Схема изменения момента инерции тела. Стало быть, инертность тела при вращении зависит не только от массы, но в большей степени от распределения этой массы относительно оси вращения. Мерой инертности тела при вращении является осевой момент инерции I, равный сумме произведений масс т всех частиц тела на квадраты их расстояний h от оси вращения. Осевой момент инерции играет при вращательном движении ту же роль, что и масса при поступательном (прямолинейном), и таким образом, он является мерой инертности (инерции) тела при вращательном движении I =∑ m * h2 (3/1)». На первый взгляд это выглядит очень научно, но это если не обращать внимания на парадоксы этой науки, которая ставит инертность в зависимость от правила рычага. Сейчас мы убедимся, что понятие софистика, которое так любит употреблять профессор Гулиа в отношении таких гигантов физики, как, например, Галилей (см. гл.1.1.), больше подходит самому популяризатору классической науки профессору современной физики, доктору физики Гулиа Н. В. Профессор Гулиа явно лукавит в отношении классического момента, говоря о трудностях раскручивания стержня якобы за сам стержень. Дело в том, что классический момент силы официально действует именно на текущем радиусе, на котором расположены грузы, что однозначно следует из уравнения моментов и его вывода. Следовательно, классическая физика раскручивает систему не за сам стержень, а прикладывает силу непосредственно к грузам, на их текущем радиусе. При этом без учёта затрат на образование центробежной силы раскручивать грузы за сами грузы с одинаковым линейным ускорением до одинаковой угловой скорости абсолютно одинаково легко или одинаково тяжело на любом радиусе. А с учётом затрат на преобразование движения по направлению раскручивать систему на больших радиусах ещё и легче, чем на малых. А вот время раскрутки на разных радиусах будет разное. Но Гулиа о времени ничего не говорит, потому что если разобраться со временем, то выяснится, что если раскручивать грузы до одинакового угла с одинаковым ускорением и соответственно с одинаковым усилием, но на разных радиусах, то понадобится разное время. Если выполнить задачу за одинаковое время, то интенсивность раскручивания, выражающаяся в силе и ускорении, будет больше на бОльшем радиусе, т.к. на большем радиусе окружная длина пути в прежнем угловом диапазоне будет больше, чем на меньшем радиусе. Причём поскольку в классическом раскручивании сила привязана именно к текущему радиусу, то формально классическая динамика вращательного движения не связана с правилом рычага. В этом и состоит её главное противоречие динамике Ньютона, которое и приводит к искажению физических величин динамики Ньютона. На бОльшем радиусе нам самим приходится быть значительно проворнее и прикладывать большую силу с бОльшим ускорением, чтобы успеть вовремя в том же угловом диапазоне, но на значительно большем отрезке пути. Естественно, что и момент инерции в этом случае привязан исключительно только к нашей собственной расторопности, а вовсе не к физической инертности массы. При этом увеличение инертности только кажущееся по сравнению с неизменным угловым диапазоном. По сравнению с увеличенной длиной пути, преодолеваемого за то же время, инертность осталась на прежнем уровне в полном соответствии с реальной массой. Увеличилась только интенсивность движения. В мерной динамике вращательного движения бОльшая сила приложена именно на меньшем радиусе, что в точности соответствует правилу рычага. При этом бОльшая интенсивность на бОльшем радиусе обеспечивается автоматически за счёт бОльшей длины плеча-радиуса. Но теперь мы должны проявить уже не бОльшую проворность, а приложить бОльшую силу на меньшем плече рычага, что и создаёт эффект возросшей инертности той же массы. Для большого радиуса даже такое виртуальное объяснение не доступно, т.к. на большем радиусе явно просматривается не увеличение инертности, а именно увеличение интенсивности движения, что никак не связано с правилом рычага на малом радиусе. К тому же правило рычага, на котором и основана мерная динамика, не искажает физические величины динамики Ньютона. Ранее в главе (2.) мы показали, что система измерения физических величин LT, которая получена путём умножения закона тяготения Ньютона на гравитационную постоянную противоречит истине, т.к. в соответствии с законом сохранения истины общие множители являются лишними для истины. Уравнение моментов так же получено умножением истинного второго закона Ньютона на перпендикулярный силе радиус, который в соответствии с законом сохранения истины является лишним для истины под названием второй закон Ньютона. Кроме того, плечо-радиус противоречит также работе перпендикулярной к нему силы. Все приведённые выше противоречия и даже абсурд классической динамики вращательного движения свидетельствует о том, что уравнение моментов, в котором лишние для второго закона Ньютона множители – радиусы входят в состав новых по сравнению с динамикой Ньютона переменных, противоречит закону сохранения истины и второму закону Ньютона. Причём новая по сравнению со вторым законом Ньютона истина в виде уравнения моментов в физике не подтверждена ни правилом рычага, ни работой перпендикулярной плечу силы, о чём свидетельствуют его многочисленные противоречия, приведённые выше. Более того, в главе (4.3.) будет показано, что переменный радиус изменяется совсем по другому закону, чем расстояние, на котором осуществляется работа силы при движении под действием самой этой силы, что противоречит физическому смыслу преобразования напряжение–движение, т.е. самому понятию работа–энергия, на котором собственно и основан вывод уравнения моментов. Это ещё раз подтверждает абсурдность классической динамики вращательного движения. Не имея возможности объяснить весь этот абсурд с точки зрения динамики Ньютона, Гулиа лукаво свёл своё объяснение фактически к правилу рычага, в котором естественным образом объясняются все, противоречащие динамике Ньютона чудеса классической динамики вращательного движения. В том числе и не имеющий физического смысла момент инерции, в котором инерция якобы зависит от радиуса! Причём уличить таких профессоров в лукавстве очень сложно, т.к. их высказывания всегда обтекаемы. Гулиа ведь не говорит прямо, что в соответствии с правилом рычага крутить грузы нужно именно за стержень. При этом в масштабе времени одинаковых угловых перемещений на разных радиусах изменится не инерционность массы, а только интенсивность перемещения грузов, для чего естественно требуется и большая сила. Это сразу же позволило бы усомниться в правоте Гулиа и классической динамики вращательного движения насчёт изменения инерционности вращающейся системы в виде момента инерции. Однако парадоксы уравнения моментов таким мелким мошенничеством не разрешить. В реальной действительности никакой мифической инерционности вращательного движения в виде несуществующей в природе физической величины – момент инерции, нет. Всё объясняется правилом рычага, отсутствующем в классической динамике вращательного движения. Физически же инерция вращательного движения, так же как и в прямолинейном движении, определяется только инертной массой вращающегося тела. Первая степень радиуса в классическом выражении для момента инерции определяется связью углового ускорения (скорости) с линейными единицами через радиус (а = ε * r). В результате при неизменном угловом ускорении пропорционально радиусу увеличивается его линейный эквивалент и соответственно сила, определяющаяся линейным ускорением. Это и создаёт эффект дополнительной инерционности неизменного углового перемещения, но с большим радиусом пропорциональной первой степени радиуса. А вторая степень радиуса связана с работой силы на участке окружности равном радиусу (F * r = m * а * r = m * ε * r * r). В этом случае момент растёт уже не за счёт силы пропорциональной радиусу, как в первом случае, а за счёт расстояния, пропорционального радиусу, на котором работает сила. Это создаёт эффект дополнительной инерционности неизменного углового перемещения, но с большим радиусом пропорциональной второй степени радиуса. Как видите, момент силы это обыкновенная работа в динамике Ньютона, а момент инерции в динамике Ньютона объясняется правилом рычага и работой на расстоянии равном радиусу. Так что никакой особой динамики вращательного движения собственно и нет. Классическая лже динамика вращательного движения влечёт за собой не только серьёзные физические, но и серьёзные количественные противоречия. Например, применение классической динамики вращательного движения к явлению Кориолиса приводит не только к искажению его физического смысла, но и к изменению количественного результата динамической силы и ускорения Кориолиса (см. гл. 3.4.). А это уже подрывает физические основы всей классической теоретической механики, т.к. явление Кориолиса фактически лежит в основе любого криволинейного движения, являющегося основным объектом изучения теоретической механики. А вот в мерной динамике вращательного движения трудности раскрутки связаны исключительно только с физическим действием правила рычага. Мерная динамика понятна даже школьникам, которые уже прошли правило рычага, в то время как классическая динамика вращательного движения не имеет разумного физического объяснения в принципе. Все эти вопросы профессор Гулиа или не видит или умышленно не освещает. Да это и неудивительно, иначе он никогда не стал бы профессором такой удивительной «парадоксальной физики…». Но мы не станем голословно упрекать профессора в приспособленчестве. Ведь всё может быть совсем наоборот. Может быть, такой парадоксальной физику и сделали такие профессора? | |
| Просмотров: 733 | |
| Всего комментариев: 0 | |