Авторы из Удмуртии (maholet.aero.ru) утверждают, что «формула ускорения Кориолиса при движении по направляющей завышена в два раза», но соглашаются, что «сила Кориолиса количественно верна», а также считают, что для небесной механики в два раза завышено не только ускорение Кориолиса, но и сила Кориолиса. Мы солидарны с авторами по всем перечисленным выше позициям в целом, кроме некоторых деталей.
Приведем оригинальный текст:
«3.4.1. Замечания о силе Кориолиса
Ошибка заключается в том, что применяется теорема Кориолиса, которая годится лишь для грубого описания случаев движения тела в «жёсткой» трубке. Эта трубка (или канал) движутся с постоянной угловой скоростью ω, что неприемлемо для свободного движения тела, когда угловая скорость изменяется, как и в данном случае со стулом.
Теорему Кориолиса ошибочно применяют при анализе отклонений падения тел на землю, например, в шахту. Опытные данные подгоняют под теорему, как и аналогичные задачи в учебниках.
Сила Кориолиса определяется по формуле (жирным шрифтом выделяем вектора):
Fк = - aк · m = -2 ω · Vr · m ,
где Vr – радиальная скорость движения тела массой m, ω – его угловая скорость. Это в 2 раза больше, чем при свободном движении тела. Направления ускорения и силы Кориолиса противоположны. При свободном же движении сила и ускорение имеют одно направление.
Применение теоремы Кориолиса для свободного движения (например, планеты) не соответствует закону сохранения энергии.
Ускорение у Кориолиса завышено в 2 раза ошибкой при взятии производной вектора переносной скорости, из-за отрыва от физики.
Сила Кориолиса (при движении в трубке) количественно верна, но не обоснована физически. Половина силы Кориолиса, действительно, является силой инерции: при приближении к центру вращения тело тормозится трубкой, при удалении – разгоняется. Другая же половина силы обусловлена действием центробежной силы, точнее, её проекцией на направление, перпендикулярное радиусу движения в плоскости орбиты (о ней будем говорить далее). Эта половина силы не даёт ускорения – не позволяет трубка. Сила Кориолиса – это сумма двух различных сил».
Авторы не приводят графическое пояснение, поэтому, чтобы прокомментировать приведенный выше оригинальный текст, проиллюстрируем точку зрения авторов графически на Рис. 10.1. Центробежная сила (Fц), по мнению авторов, направлена вдоль геометрического радиуса кривизны (О1,В) дуги (ВС). Авторы полагают, что вторая половина силы Кориолиса, обусловлена силой Fц1 (см. Рис.10.1).
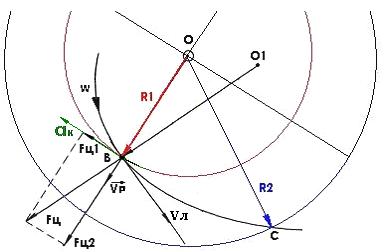
Рис. 10.1
В главе 3.5 показано, что с позиции классической модели вращательного движения принципиально невозможно обнаружить тангенциальные силы, возникающие при «свободном» движении с изменяющимся радиусом, т.к. радиальная сила имеет проекцию только на реальную траекторию поворотного движения и не имеет проекций на строго круговую траекторию переносного вращения. Авторы из Удмуртии попытались преодолеть этот недостаток общей кинематики вращательного движения, через определение центробежной силы (Fц) вдоль геометрического радиуса поворотного движения. При этом они получили-таки проекцию центробежной силы на касательную к окружности переносного вращения в виде тангенциальной силы (Fц1). Однако это решение столь же не физическое и абсурдное, как и классическая модель вращательного движения.
Безусловно, любое произвольное криволинейное движение может быть представлено в виде совокупности равномерных вращательных движений по вписанным окружностям с постоянным геометрическим радиусом. Именно так мы с вами и поступили при определении абсолютного ускорения произвольного криволинейного движения (см. главу 7.3). Однако при этом проектировать силы и ускорения, проявляющиеся вдоль геометрического радиуса на реальную траекторию физически неправомерно, т.к. все соседние точки реальной траектории в таком представлении принадлежат другим вписанным окружностям, т.е. другим движениям.
Таким образом, если мы академически представили движение точки (В), как движение по вписанной окружности с геометрическим радиусом (О1В), то его центробежная сила (Fц) уже не может иметь проекции на касательную к этой окружности в виде тангенциальной силы, т.к. они взаимно перпендикулярны. В этом направлении, но вдоль касательной к реальной траектории действует истинная сила Кориолиса, которая является проекцией центростремительной силы (силы тяготения), направленной вдоль физического радиуса (ОВ). Это и есть истинная сила Кориолиса.
Истинная сила Кориолиса выполняет свою функцию именно вдоль линии проявления линейной скорости движения, направленной по касательной к реальной траектории. При радиальном движении в сторону от центра тяготения именно эта сила реально тормозит тело, и именно эта сила ускоряет его при радиальном движении к центру тяготения. В соответствующем направлении в каждом из этих случаев проявляется и истинное ускорение Кориолиса, которое действительно вдвое меньше классического. Понятно, что при этом меняется и виртуальная для поворотного движения линейная скорость переносного вращения.
Авторы из Удмуртии нашли лишь оригинальный способ определить проекцию результирующей силы вращательного движения на круговую траекторию переносного движения. Классическая физика в лице Хайкина С. Э. так и не смогла этого сделать (см. главу 3.5), т.к. классическими методами это сделать принципиально невозможно. Но даже оригинальный способ, найденный авторами из Удмуртии, не проясняет физический механизм образования такой проекции. Истинная сила Кориолиса физически может быть привязана к тангенциальному направлению по отношению к виртуальным окружностям переносного вращения только через проекцию энергетического влияния радиальной силы на тангенциальное направление, как показано в главе 3.5.
Причем энергетическая проекция это наше академическое нововведение специально для разрешения противоречий классической физики, которой непременно хочется, чтобы сила Кориолиса действовала вдоль геометрической окружности приносного вращения. Но она не может это обосновать, т.к. радиальная сила не имеет проекций на переносную окружность. На окружность может иметь проекции только результирующая сила поворотного движения, которая направлена вдоль касательной к реальной траектории, и на формирование которой естественно оказывает непосредственное влияние радиальная сила. Вот так и появилась академическая, но физически обоснованная проекция энергетического влияния или энергетическая проекция.
Физическая наука не может игнорировать общую кинематику криволинейного движения на макроуровне. В этом мы полностью согласны с классической физикой, т.к. на макроуровне проявляется исключительно общая кинематика любого движения. Но раз уж мы вынуждены мириться с общей кинематикой криволинейного движения, динамику которой векторная геометрия определить, бессильна, то без энергетических проекций в современной физике не обойтись. Во всяком случае, это позволит избавиться от абсурдных противоречий классической физики в теоретическом обосновании динамики криволинейного движения на основе его общей кинематики.
Следующее замечание. Авторы пишут: «Половина силы Кориолиса, действительно, является силой инерции: при приближении к центру вращения тело тормозится трубкой, при удалении – разгоняется». Но в соответствии с концепцией классической физики фиктивные силы инерции не могут ничего ни разгонять, ни тормозить. В классической физике это просто абстрактная математическая реакция. Разгоняет и тормозит тело в трубке только реальная поддерживающая сила, а инерционная половина силы Кориолиса это только реакция на поддерживающую силу.
Это же замечание актуально и для представления авторов о второй половине силы Кориолиса: «Другая же половина силы обусловлена действием центробежной силы, точнее, её проекцией (Fц1) на направление, перпендикулярное радиусу движения в плоскости орбиты». Но здесь сложнее. Здесь авторы намешали в кучу и реальные и фиктивные силы. Эта вторая половина существует и в отсутствие поддерживающей силы, как, например, в небесной механике. Об этой половине авторы говорят, что она совпадает по направлению со своим же ускорением (на рисунке зелёная стрелка, совпадающая с (Fц1)): «При свободном же движении сила и ускорение имеют одно направление». Но тогда это самая что ни на есть обычная сила, т.е. она не может быть проекцией фиктивной центробежной силы, направленной хоть вдоль физического радиуса, хоть вдоль геометрического радиуса!
Именно эта сила тормозит и ускоряет тело в отсутствие поддерживающей силы, в том числе и в небесной механике и направлены эти действия противоположно поддерживающей силе при движении в трубке. У авторов же эта сила такая же фиктивная, как и первая половина! По крайней мере, так следует из их текста дословно, ведь у них ускоряет и тормозит тело именно первая половина, про вторую они уже так не говорят. Правда, в дальнейшем через воздействие эфира они поясняют, что центробежная сила это вполне реальная сила. Но всё же это не только словесная неразбериха. Ниже будет показано, что воздействие эфира по типу подъёмной силы крыла играет в описываемом процессе второстепенную роль. Главная роль принадлежит тяготению.
Далее авторы утверждают: «Сила Кориолиса (при движении в трубке) количественно верна, но не обоснована физически». Это так же не совсем верно. Сила Кориолиса не только не обоснована физически, но и количественно не верна. Как утверждают сами авторы, вторая половина уравновешена трубкой: «Эта половина силы не даёт ускорения – не позволяет трубка». Но в динамике неуравновешенного движения уравновешенные силы не участвуют. Поэтому количественно верно только напряжение Кориолиса. Да и Кориолиса ли это напряжение, если за истинную силу толи Кориолиса, толи Кеплера в её составе принимать только вторую половину? Впрочем, это не вина авторов. Неумение чётко излагать свои мысли это наша общая беда.
Далее авторы рассматривают движение свободнолетящего тела под действием центральной силы. Замечания к ним все те же, что и по силе Кориолиса. Но их рассуждения заслуживают внимания, потому что авторы в принципе находятся на правильном пути. Поэтому приведем еще одну обширную цитату из их работы:
«3.4.2. Свободное движение
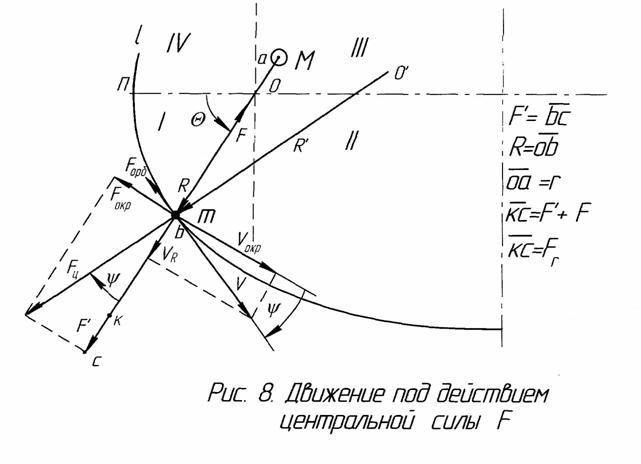
На рис.8 тело массы m под действием центральной силы F (с центром в точке О) движется по кривой L переменного радиуса кривизны R' с центром кривизны О' со скоростью V. Точка П – перицентр орбиты L. Скорость тела, находящегося в точке в, разложим на 2 составляющие: VR –радиальная, Vокр – перпендикулярно радиусу обиты R .
На тело m, помимо сил инерции, действуют 2 силы: центральная F (или центростремительная) и центробежная сила Fц. Эту последнюю силу нельзя отнести к силам инерции (см. предыдущий параграф 3.3). В небесной механике считается, что планеты движутся под действием одной центральной силы, что окружное (азимутальное, трансверсальное) ускорение равно нулю (спис. лит.- 46), что планеты имеют только центростремительное ускорение (с.л. 59, 76), направленное всегда к центру тяготения по радиусу. Однако, вечно «ускоряясь», ни одна из них не приблизилась к Солнцу.
Что же это за алхиметрия?! Если планета не имеет окружного ускорения, то, что же заставляет тогда её изменять окружную и угловую скорость, например, при переходе от апоцентра к перицентру?
Итак, центробежную силу Fц , действующую по радиусу кривизны, разложим на 2 составляющие: F' – по радиусу орбиты (радиальная составляющая), Fокр – перпендикулярно этому радиусу – окружная составляющая.
С противоположной стороны от центра О в точке а движется центральное тяготеющее тело М (например, Земля, если m – Луна) с меньшим радиусом орбиты RM = Оа.
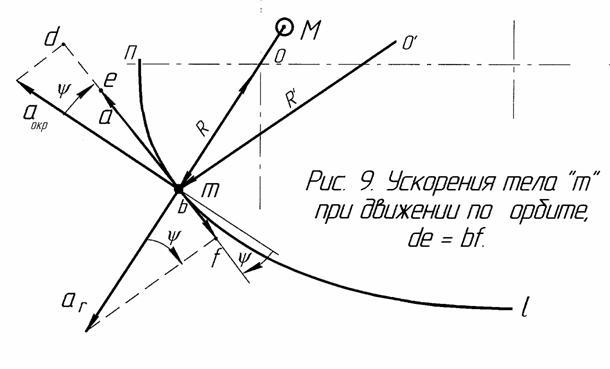
На рис. 9 представлены ускорения, действующие на тело m. О них поговорим позднее.
Угол ψ – это угол между вектором орбитальной скорости V и вектором окружной скорости Vокр. Он положителен, если VR – положительна. Угловая скорость ψ' положительна, если угол ψ растёт. При движении в I четверти (как на рисунках) и в IV четверти центробежная составляющая F' по модулю больше центральной силы F на величину кс. Они равны при углах истинной аномалии θ = 90º и 270º, что следует из расчётов. Во II и III четвертях F'<F. За счёт разницы этих сил и возникает радиальное ускорение ar , которое два раза меняет свой знак за 1 оборот тела по орбите. В I и IV четвертях это ускорение положительно – направлено от центра. Скорость положительна также при направлении от центра.
В I и II четвертях тело m, удаляется от центра О, окружная сила Fокр направлена назад – тело тормозится (в окружном и орбитальном направлениях). В III и IV четвертях (движение от апоцентра к перицентру) - ускоряется. Эту окружную силу Fокр и заменяют в небесной механике и в ряде земных задач ошибочно силой Кориолиса.
Определим величину окружной силы и окружного ускорения .
1 вариант вывода. Величина этой силы была определена из сравнения работ центральной и орбитальной сил. Производилось также сравнение работы орбитальной силы с изменением кинетической энергии тела m (например, для случая на рис.10) с учётом того, что при отсутствии момента внешних сил момент количества движения постоянен (есть теорема), то есть в скалярном виде
L = m · V · R · cosψ = const.
Задача решена на частных примерах и в квадратурах. Получилось, что все три энергии равны, если окружная сила (в скалярном виде):
Fокр = aокр· m = -VR · ω · m.
Здесь: окружное ускорение aокр= -VR · ω ,
ω- угловая скорость.
Знак минус (-) означает, что при положительной радиальной скорости VR (движение от перицентра к апоцентру - подъём) ускорение и сила отрицательны, то есть тело тормозится.
2 вариант. Величину окружной силы можно определить из 2 закона Кеплера, который запишем в скалярной форме:
Ś = ½ R V cos ψ = ½ R Vокр = const.
Секториальная скорость Ś постоянна, поэтому её производная по времени равна нулю:
Ś't = ½ [ R't ´ Vокр+R · (Vокр)'t ] = 0.
Здесь:
R't = VR - радиальная скорость, поскольку R - скаляр;
( Vокр)'t = aокр - окружное ускорение;
Vокр = ω·Rокр = θ' · Rокр .
Тогда уравнение можно записать так:
VR·ω · Rокр +Rокр ·aокр = 0 .
Сократив на Rокр, получим :
aокр = -VR · ω. ( формула 3.4.2.1)
Окружная сила, с учётом 2 закона динамики, будет равна:
Fокр = aокр · m = - VR · ω · m . (форм.3.4.2.2)
Вновь получили такое же выражение окружного ускорения и окружной силы, что и в 1 варианте.
Ньютон, Лагранж и их последователи до наших дней допускают ошибку при выражении секториальной скорости:
Ś = ½ RVокр.
Её просто заменяют геометрическим выражением:
S = ½ R2окр ω,
где радиус Rокр - фиксированная величина (в действительности R ≠ Rокр) .
При взятии производной это даёт другой результат – окружное ускорение aокр получается с двойкой, как у Кориолиса, но с другим знаком.
3 вариант. Вместо 2-го закона Кеплера (во втором варианте вывода) можно взять закон постоянства момента количества движения в скалярной форме: M = m V R cosψ. Результат опять будет таким же.
Таким образом, при орбитальном свободном движении тело имеет окружное (азимутальное) ускорение аокр под воздействием окружной силы эфира
Fокр = -VR · ω · m.
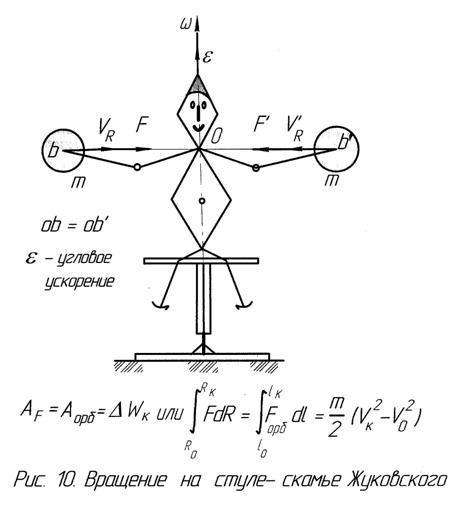
Когда человек с гантелями вращается на стуле (рис.10), подтягивая их к себе, он ускоряется этой окружной силой. Этой силе приходится здесь разгонять не только гантели, но и человека со стулом. Поэтому ускорение разгона будет меньше, чем аокр. Следовательно, в общем случае тело испытывает напряжённость окружной силы:
аокрн = Fокр / m
А само ускорение тела будет
aокр = Fокр ׃ mпр ,
где mпр - приведённая масса тела (стандартное понятие).
Определим связь между ускорениями свободного тела m (согласно рис.8 и 9).
Продифференцируем по времени скорости:
Vокр = Vcosψ, VR = Vsinψ.
Получим значения окружного и радиального ускорений:
аокр =(Vокр)' =V'cosψ - V sinψ ·ψ' = a cοs ψ - Vψ'sinψ ,
где a =V' - орбитальное ускорение;
ar =(VR)' =V'sinψ+Vcosψ·ψ' = asinψ +Vψ'cosψ
- радиальное ускорение, направлено по радиусу орбиты; оно положительно, если направлено от центра.
После исключения произведения Vψ' из обоих выражений и несложных преобразований получим соотношение ускорений (в общем случае при несвободном движении - напряжений):
a =aокрcosψ +arsinψ (формула 3.4.2.3).
Орбитальное ускорение равно сумме проекций окружного и радиального ускорения на направление касательной к траектории.
Орбитальная сила имеет направление ускорения и равна:
Fорб = ma (3.4.2.4).
Для вычисления радиального ускорения надо cумму центробежной составляющей и центральной (центростремительной) сил (с учётом их знака) разделить на массу тела:
ar = (F/+F)/m = (F/-|F|) /m =Fr /m (3.4.2.5).
Здесь Fr является радиальной силой, под действием которой и происходят радиальные перемещения и изменения скорости.
Умножим равенство 3.4.2.3 на массу тела m, получим:
ma =maокрcosψ +marsinψ.
Или, учитывая предыдущие соотношения и определения:
Fорб =Fокрcosψ +Frsinψ (3.4.2.6).
Орбитальная сила равна сумме проекций окружной и радиальной сил на направление касательной к траектории.
Таковы реальные физические ускорения и силы, действующие на движущееся тело под действием центральной силы.
Заметим, что при определении ускорений производная бралась не от вектора скорости (как принято в классической механике), а от величины скорости. Как уже отмечалось в нашей работе (пар.3.3), ускорение – это изменение скалярной величины скорости (или просто – величины скорости). Направление ускорения определяется направлением ускоряющей силы.
Как видно, мы не обнаружили центростремительного ускорения и в данной задаче. Есть радиальное ускорение, которое может быть направлено как к центру, так и от центра. Оно соответствует реальным перемещениям и изменениям скоростей тела. Нет центростремительных ускорений, есть центростремительные напряжения, вызванные центральной силой. И это следовало бы различать. Но физико-математики с этим не считаются. И складывают ускорения с напряжениями. И иногда получают теоремы.
Ускорение – это результат действия напряжений.
Следует обратить внимание, что окружные и орбитальные силы и ускорения дают проекцию на ось апсид (большая ось орбиты), всегда направленную к перицентру.
Справедливость полученных выражений можно проверить простым численным примером движения Земли вокруг Солнца. Нами проводились различные эксперименты по вращению тел с переменным радиусом. Под действием орбитальной силы эфира раскачиваются качели, падают тела, движутся планеты, спутники и т.д..
В литературе по баллистике и небесной механике в уравнениях орбитального движения, составленных в полярных или сферических координатах, присутствуют компоненты ускорения и силы Кориолиса, что даёт погрешность в расчётах траекторий.
Лишь то, что движется по Земле (поезда, реки…) или в «трубке» с постоянной угловой скоростью, испытывает действие сил Кориолиса с учётом замечаний подпараграфа 3.4.1.
В случае свободного движения тела в поле центральной силы работает схема сил и ускорений, представленная в данном подпараграфе 3.4.2. По данной схеме раскачиваются качели, падают тела, движутся по орбитам спутники, планеты и т.д.. Маятник Фуко испытывает действие орбитальной силы, но оно не влияет на суточный период обращения плоскости качаний, поскольку действие этой силы за полупериод качания компенсируется её противоположным действием за следующий полупериод».
Мы не против признания эфира, как мировой среды и в этом отношении полностью согласны с В. А. Ацюковским (см. «ОБЩАЯ ЭФИРОДИНАМИКА»). Но речь может идти только о влиянии эфира, как дополнительного фактора, а не как фактора, образующего вращательное движение макротел. Ведь выталкивающая сила эфира появится только при разности скоростей обтекания эфиром движущегося тела.
Скорость обтекания эфиром тела движущегося равномерно и прямолинейно со всех сторон одинаковая. Для получения разности скоростей необходимо иметь установившееся вращательное движение, когда скорость обтекания со стороны центра вращения будет отличаться от скорости с внешней стороны. Значит вначале должно возникнуть вращение со всеми вытекающими последствиями, а уже потом начнет сказываться влияние эфира. Поэтому представленная авторами схема образования сил вращения правомерна только для установившегося вращения в эфирной среде. При этом силы по типу подъёмной силы, никакого заметного влияния на параметры движения не окажут.
Ну а по большому счёту все взаимодействия действительно обеспечиваются эфиром (см. главу 1.2). Только центробежная сила в подавляющей своей части это не подобие подъёмной силы крыла. Это реализация накопленной инерции (энергии) прямолинейного движения, которая выделяется при поэлементной поддержке движения. Вначале за счёт силы тяготения тормозятся (ускоряются) наиболее радиально удалённые (приближённые) от центра (к центру) тяготения элементы. При этом на них воздействуют последующие элементы. А далее осуществляется механизм явления инерции (см. главу 1.2), который и определяет ускорение и торможение движения планет по орбитам.
Относительно мнения авторов, что в небесной механике в два раза завышено не только ускорение, но и сила Кориолиса, у нас по большому счёту возражений нет. С классической точки зрения сила Кориолиса в небесной механике не действует, т.к. угловой момент в орбитальном движении не изменяется. Однако как показано в главе 3.5 и главе 4.2 именно истинная сила Кориолиса вдвое меньшая классической силы Кориолиса и определяет процесс преобразования видов вращательного движения и закон сохранения углового момента.
В целом с учётом наших замечаний мы согласны с авторами из Удмуртии практически по всем позициям. Хотя из этих замечаний следует, что авторы так и не раскрыли природу явления Кориолиса. Во многом этому мешает паразитные академические условности классической физики. Если уж условно считать силы инерции фиктивными, то:
Во-первых, необходимо честно заявить, что эта условность введена только для отражения реальной действительности на доступном сегодняшней науке уровне, когда взаимодействия на уровне мировой материальной среды пока ещё не могут быть непосредственно обнаружены. Они обнаруживаются только косвенно.
Во-вторых, для придания академическим условностям общей кинематики криволинейного движения реального физического смысла необходимо дополнить векторную геометрию энергетическими проекциями, физический смысл которых вовсе не условный. Условно только название, но зато оно сократит длинное объяснение смысла проекций энергетического влияния.
В-третьих, необходимо отказаться от порочной практики приписывать условным академическим силам инерции, хотя и с отрицательным знаком ускорения, генерируемые обычными силами. От этого возникает главная путаница между реальными и мнимыми силами и ускорениями в современной физике. Ведь ускорение Кориолиса, например, не принадлежит силе Кориолиса. Это ускорение поддерживающей силы. Тогда сразу же становится очевидным, что в классическом поворотном движении нет никакого ускорения Кориолиса. Истинное ускорение Кориолиса принадлежит истинной силе Кориолиса – Кеплера. И это вполне обычная сила и обычное ускорение.
Возможно, в отсутствие паразитных условностей или, по крайней мере, при чётком обозначении их места в природе авторы «Махолёта» выразили бы свои мысли намного яснее. Но даже их сегодняшних взглядов вполне достаточно, чтобы опровергнуть классическую версию явления Кориолиса или, по крайней мере, заставить современную науку усомниться в ней!