| Главная » Статьи » Физика и математика » Мои статьи |
Прежде чем говорить о физическом смысле арифметических операций напомним основные понятия арифметики: Операнд – величина, представляющая собой объект операции. Операции определяют действия, которые надо выполнить над операндами (+, –, ×, :). Сложение (прибавление) — одна из основных операций (действий) в разных разделах математики, позволяющая объединить два объекта (в простейшем случае — два числа). Более строго сложение — бинарная операция, определённая на некотором множестве, элементы которого мы будем называть числами, при которой двум числовым аргументам (слагаемым) a и b сопоставляется итог (сумма), обычно обозначаемый с помощью знака «плюс»: a + b. Вычитание – действие, обратное сложению (См. Сложение); задачей В. является определение одного из двух слагаемых, когда даны сумма и другое слагаемое. Данная сумма называется уменьшаемым, данное слагаемое — вычитаемым, результат действия — разностью. В области положительных чисел В. не всегда выполнимо (из меньшего числа нельзя вычесть большее). Это обстоятельство является формальным поводом для введения в арифметику нуля и отрицательных чисел; в расширенной таким образом числовой области В. всегда однозначно выполнимо. Умножение – операция образования по двум данным объектам а и b, называемым сомножителями, третьего объекта с, называемого произведением. Умножение обозначается знаком «×» (ввёл англ. математик У. Оутред в 1631) или «•» (ввёл нем. учёный Г. Лейбниц в 1698); в буквенном обозначении эти знаки опускаются и вместо а × b или а • b пишут ab. Умножение имеет различный конкретный смысл и соответственно различные конкретные определения в зависимости от конкретного вида сомножителей и произведения. Умножение целых положительных чисел есть, по определению, действие, относящее числам а и b третье число с, равное сумме b слагаемых, каждое из которых равно а, так что ab = а + а + ... + а (b слагаемых). Число а называется множимым, b – множителем. Деление – действие, обратное умножению (См. Умножение); заключается в нахождении одного из двух сомножителей, если известны произведение и др. сомножитель. Т. о., разделить а на b — это значит найти такое х, что bx = а или xb = а. Результат Д. х называется частным, или отношением, a и b. Заданное произведение а называется делимым, а заданный множитель b — делителем. Для обозначения Д. употребляют знаки двоеточия (а : b) или горизонтальной (иногда наклонной) черты (a/b). Натуральные числа (естественные числа) — числа, возникающие естественным образом при счёте. Последовательность всех натуральных чисел, расположенных в порядке их возрастания, называется натуральным рядом. Существуют два подхода к определению натуральных чисел — это числа, возникающие при: подсчёте (нумерации) предметов (первый, второй, третий) или при обозначении количества предметов (нет предметов, один предмет, два предмета). В первом случае ряд натуральных чисел начинается с единицы, во втором — с нуля. Не существует единого для большинства математиков мнения о предпочтительности первого или второго подхода (то есть считать ли ноль натуральным числом или нет). В подавляющем большинстве российских источников традиционно принят первый подход. Нуль – (нем. Null, от латин, nullus – никакой). Арабская цифра, сама по себе, ничего не значащая, но показывающая отсутствие того разряда цифр (в нумерации), на месте которого она стоит (правильнее сказать отсутствие цифр в разряде – авт.); поставленная после значащих цифр обозначает десятки, сотни, тысячи и т. д. Для простоты будем рассматривать действия с натуральными числами. *** Хотя математика является всего лишь языком физики, практически все математики давно забыли об этом и провозгласили математику царицей наук, стоящей даже выше физики. Поэтому мы предлагаем вашему вниманию давно забытые математиками физические основы арифметических операций и причины, по которым математики иногда вполне обоснованно нарушают их в пользу своих математических абстракций. Однако при этом сами математики, как это ни странно, уже не в состоянии объяснить правомерность своих же собственных правил по причине отрыва от физики. В природе количество предметов изменяется либо в процессе физико–химических взаимодействий материи, либо в результате её механического движения. При этом любое изменение количества предметов должно строго соответствовать закону сохранения материи и энергии, что подразумевает изменение количества в строгом соответствии с реальными физическими действиями с ними. В арифметике определение общего количества предметов осуществляется путём их сквозной нумерации (счёта) с присвоением каждому последующему элементу счёта порядкового номера на единицу большего, чем предыдущий. При этом сам процесс счёта фактически представляет собой операцию сложения, простейшим слагаемым которого является одна единица счёта или нумерации. А суммой является последний порядковый номер счёта. Совершенно очевидно, что сквозная нумерация не зависит от любых внутренних перестановок предметов внутри их общей суммы в любом их сочетании и количестве, что и определяет все известные свойства сложения и их соответствие законам природы. На этих физических свойствах собственно и основаны все остальные арифметические операции, являющиеся всего лишь различными алгоритмами сложения или обратного ему действия вычитания. Таким образом, сложение является базовой операцией определения количества чего–либо в природе. В математике существуют также более сложные математические операции: возведение в степень, извлечение корней, логарифмы, экспоненты и т.д. Однако все они так или иначе построены на простейших арифметических операциях, т.е. в конечном итоге на базовом сложении, что отражено в определении их количественного результата «столбиком». Таким образом, базовой арифметической операцией, лежащей в основе всех математических операций, является операция сложения, физической основой которой является сквозная нумерация или счёт. Рассмотрим физический смысл простейших арифметических операций на примере операций с нулём, которым обозначают отсутствие количества предметов счёта и действий с ним, т.к. именно такие операции и вызывают наибольшее количество вопросов по физическому смыслу арифметических операций. Итак, обо всём по порядку. Сложение. По определению общая сумма должна определяться общим счётом, т.е. последовательной нумерацией предметов счёта, содержащихся, как минимум в двух числах, что определяет свойство бинарности сложения. При этом в случае сложения одного значащего числа с нулём свойство бинарности формально нарушается, т.к. нуль – это символ, обозначающий отсутствие числа. Однако вопреки официальному определению сложения и в частности свойству бинарности, суммой в математике однозначно признаётся даже один единственный значащий операнд, о чём свидетельствует существующее сложение с нулём: 0 + Х = Х + 0 = Х По официальной версии один операнд просто не с чем складывать. Однако физически даже один операнд имеет собственную сквозную нумерацию, конечный номер которой определяет его собственную сумму. Она же фактически является и общей суммой операции сложения с нулём, если уж признавать такую не бинарную операцию с нулём правомерной. Однако, как это ни странно, официальная математика отрицает это вполне правомерное физическое объяснение свойства бинарности в операциях сложения с нулём.
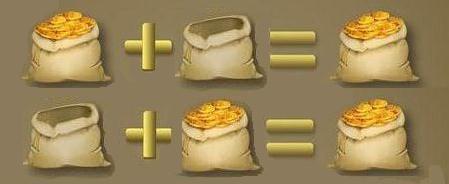
Рис. 6.1.1 На рисунке (6.1.1) показано, что сумма нуля со значащим операндом, представляющим собой мешок с деньгами, равна собственному счёту денег в мешке при любом порядке сложения этих операндов. Некоторые наши оппоненты утверждают, что результат такой фактически несостоявшейся операции с бездействующим и беспредметным нулём не может считаться результатом самой операции, как таковой, т.к. она не состоялась.
Но во–первых, при этом сохраняется результат сквозного счёта значащего операнда. А, во–вторых, результат – это итоговое знание существующей реальности, которое включает в себя, в том числе и знание того, состоялось ли что–то или не состоялось.
Что касается бинарности, то даже, если единственный значащий операнд представляет собой одну единственную единицу счёта, например, одну монету, то и это теоретически не отменяет суммарного итога такой не бинарной операции, поскольку одна единица счёта одновременно является первичным структурным элементом суммы. А поскольку конечность деления материи на сегодняшний день наукой не установлена, то вопрос бинарности это ещё и вопрос выбора единиц измерения или масштаба счёта. Даже одиночные предметы перестают быть единицами счёта при изменении его масштаба. Таким образом, бинарность в физике – это всего лишь вопрос выбора единиц измерения предметов счёта, а в математике – масштаба единиц счёта, мельчайшая из которых в любом случае является элементом счёта и соответственно первичным структурным элементом суммы. Некоторые математики не видят нарушения свойства бинарности в операциях сложения с нулём совсем по другой причине. Они считают нуль таким же полноправным числом, как и значащие числа, а значит и полноправным операндом операции сложения. Однако не меньшее количество математиков так не считают. Но математика, как язык физики, не может опираться на личные предпочтения математиков. Поэтому здесь и далее мы будем исходить только из физических соображений. Число – это не просто второе лингвистическое название, т.е. синоним операнда. Физически любое число отражает количество предметов. И хотя официально цифры в математике не считаются числами, количество заложено также и во все цифры от 1 до 9, кроме нуля. Нуль – это единственная цифра, или символ, обозначающий отсутствие количества по определению. Следовательно, физически, а значит и математически нуль – это не число. Нуль – это цифра, символизирующая отсутствие чего–либо, т.е. это символ несуществующей сущности, в том числе и несуществующего действия. Но дело вовсе не в названии. Даже если назвать нуль числом, он так и останется особым, пустым «числом», обозначающим пустой операнд, не способный ничего изменить ни в какой операции. В представленной выше иллюстрации (см. Рис. 6.1.1) таким пустым операндом является сам мешок, который не способен изменить общий счёт денег, задействованных в операции. Можно, конечно, дорисовать нуль или нулевой пустой мешок и в правой части равенств, изображённых на рисунке (6.1.2), однако на суммарном количестве денег это никак не отразится. Поэтому в правой части пустые мешки, эквивалентные пустому числу нуль, мы просто опускаем.
Рис. 6.1.2 То же самое можно принципиально сделать и в левой части, в которой пустой мешок или нуль сохранён исключительно только для обозначения последовательности математических преобразований исходного выражения, в результате которых его члены могут и обнуляться, в том числе. При этом в математике нулевые члены без каких–либо противоречий физическому счёту могут быть опущены только в операциях сложения и вычитания. В умножении принципиально такая же операция опускания одинаковых членов выполняется делением на одинаковые члены, что уже принципиально отличается от простого «опускания» и соответственно называется несколько другим словом — «сокращение». Причём в отношении нулевых членов эти различия принципиально одинаковых действий над принципиально одинаковыми операциями, опирающимися на общее базовое сложение, необъяснимы с физической точки зрения. Если в сложении и вычитании сократить или просто опустить нулевые операнды можно безо всяких последствий для итогового счёта или суммы, то в умножении и делении просто так без последствий избавиться от несуществующих операндов, обозначенных нулём, не получится. Существующее умножение на нуль совершенно не естественным, т.е. не физическим образом обнуляет весь предыдущий счёт, а сокращение или деление на нуль в математике вообще запрещено, что противоречит физическому смыслу базовой операции сложения! Ё! Более подробно мы рассмотрим это вопрос ниже в разделе «умножение» и «деление». Вычитание — обратно сложению. В вычитании ничего не значащая по определению цифра – нуль также не считается нарушением свойства бинарности: Х — 0 = Х + (–0)) и (0 — Х = 0 + (–Х) Справедливость этих равенств не зависимо от свойства бинарности проиллюстрировано на рисунке (6.1.3). Конечно же, последнее равенство на рисунке (6.1.3) можно представить, как мешок с деньгами со знаком минус или как пустой мешок, что означает мнимое число денег, т.е. долг. Тем не менее заметим, что вернуть–то в любом случае нужно положительное количество денег. Следовательно, мнимое отрицательное число долга количественно по абсолютной величине равно значащему операнду, что и отражено в последнем равенстве на рисунке (6.1.3) без знака минус.
Рис. 6.1.3 На рисунке (6.1.4) символическая запись долга показана в виде мнимого отрицательного мешка с деньгами в верхнем равенстве или в виде пустого мешка в нижнем равенстве. Это вопрос всего лишь условных обозначений, но никак не физики процесса.
Рис. 6.1.4 Но даже формальное нарушение свойства бинарности в базовом сложении и вычитании с нулём – это ничто по сравнению с физическими противоречиями арифметических операций умножения и деления с нулём. Несмотря на то, что эти операции ничем принципиально не отличаются от базовой для них операции сложения, пустое число нуль в них является настолько значимым, что только он один целиком и полностью определяет результат счёта даже для значимых операндов. Итак, перейдём к физическому смыслу операций умножения и деления на нуль. Умножение. По определению умножение – это сложение одинаковых операндов равных по величине умножаемому в количестве равном множителю. Как видно, по своему физическому смыслу операция умножения, которую можно представить в виде сложения одинаковых операндов, ничем принципиально не отличается от операции базового сложения. Однако если в сложении и вычитании нуль не влияет на конечный результат, то в результате операции умножения значащего числа с нулём получается нуль, что совершенно необоснованно с физической точки зрения: Х * 0 = 0 * Х = 0 Можно показать, что если нуль обозначает величину умножаемого (0 * Х), то аналогия классического умножения с нулём, как алгоритма повторяющегося сложения, в котором есть (Х) одинаковых нулевых слагаемых со сложением, хотя бы формально сохраняется: 0 * Х = 0 + 0 + … + 0 = 0 Это является самым распространённым в математике формальным доказательством нулевого результата при умножении на нуль. А формальность этого доказательства заключается в следующем:
Во–первых, повторение несуществующей сущности возможно только абстрактно математически. В реальной действительности, как ничто ни повторяй, ничто и получится. Точнее ничего не получится. Поэтому нулевой символ, обозначающий отсутствующую сущность, так и останется единственным и не повторённым, причём только в начальных условиях операции, т.к. саму операцию с нулём следует считать не состоявшейся. А результат этой не состоявшейся операции ничем не будет отличаться от результата операции базового сложения с нулём: 0 + Х = 0 * Х = Х Во всяком случае значащий операнд x, присутствующий в исходных условиях игнорировать, как ничего не значащий 0, нельзя. Тем более что раз операция не состоялась, то с (х) в итоге ничего не может произойти в принципе. Во-вторых, само по себе не повторение должно оставлять всё, что есть без изменения, т.к. нет никаких физических оснований считать, что ни разу не повторённый значащий операнд вдруг исчезает, превратившись в нуль, безо всяких действий над ним. При этом, чтобы факт несостоявшейся операции никого не смущал, операцию с бездействующим нулём целесообразно считать вполне состоявшейся охранной операцией по запрещению действия, хотя бы в противовес официальному физическому беспределу по необоснованному уничтожению значащих операндов при умножении их на нуль. В этом случае, операция умножения числа на нуль будет строго соответствовать базовой операции сложения с нулём: Х + 0 = Х * 0 = Х
Но молчат математики, нет у них вразумительного объяснения, что это за странное правило такое и откуда оно взялось. В-третьих, повторение нуля (0 * Х = 0 + 0 + … + 0 = 0) не только не возможно физически, о чём говорится в пункте 1. Это противоречит результату не повторения значащего операнда (Х * 0 = Х), т.е. фактически переместительному свойству умножения. Следовательно, более правдоподобной является охранная операция по запрещению действия с нулём, т.е. с ничем, в результате которой сохраняется (охраняется) значащий операнд (Х * 0 = Х). А невозможность повторения незначащего операнда не отменяет значащий операнд, присутствующий в начальных условиях. В–четвёртых, поскольку, как показано в первых двух пунктах, в операциях умножения и деления на нуль символ нуля физически не соответствует своей ничтожной физической сущности не только количественно, но и в качестве действия, то очевидно, что в этих операциях он наделён в классической физике не свойственными для него качествами действия искусственно вопреки своему определению.
Очевидно, что физически бездействие нуля в умножении не должно принципиально отличается от бездействия нуля в базовом для умножения сложении. Поэтому в результате умножения с нулём точно также, как и при сложении с нулём, а также при умножении с единицей, которая всего лишь оставляет то, что есть в единичном экземпляре, что также эквивалентно бездействию не только нуля, но и единицы, физически должен получаться именно значащий операнд: Х * 0 = 0 * Х = Х * 1 = 1 * Х = Х Причём это не противоречит ни физическому смыслу базового сложения, ни определению умножения, в котором естественно для классической арифметики не оговаривается эквивалентность умножения на нуль и единицу, ни определению нуля и единицы. Дело в том, что эквивалентность умножения на нуль и на единицу вовсе не означает физического равенства нуля и единицы. Равны только результаты операций с их участием. Но и в этом также нет никаких противоречий. Оставить всё, как есть при умножении на ничего не значащий нуль – это абсолютно то же самое, что и оставить то, что есть в единственном экземпляре при умножении на вполне значащую единицу. Всё выше сказанное относится, в том числе и к делению на нуль (Х / 0 = Х), что будет показано ниже в разделе «деление». А пока покажем правомерность физического умножения на нуль в нашей версии на конкретном примере. Умножение с нулём, эквивалентное умножению на единицу, а также переместительное свойство умножения, совершенно очевидно следует из сквозной нумерации базового сложения ячеек одной и той же таблицы. Естественно, что от перемены мест сомножителей, роль которых играют столбцы и строки таблицы, общее количество её ячеек, определяющееся её сквозной нумерацией, не изменится. Именно так в официальной арифметике популярно объясняют переместительное свойство умножения детям. За исключением, конечно же, умножения с нулём, о чём мы поговорим ниже. Итак, пусть имеется таблица, состоящая из (х) строк и (у) столбцов. В качестве исходных данных условимся также, что строка должна состоять как минимум из двух ячеек по горизонтали, а столбец из двух ячеек по вертикали. В противном случае количество строк или столбцов равно нулю. Это, кстати, общепринятое понимание строк и столбцов. Например, в кроссвордах строку, состоящую из (n) букв никто не называет буквами, расположенными в (n) столбцах, а вертикальную надпись никто не называет буквами, расположенными в (n) строк. Математика, конечно не кроссворды, но логика, тем не менее, вещь упрямая и универсальная. Общее количество ячеек таблицы (N) в полном соответствии с определением умножения, основанном на базовом сложении равно: N = х * у = у * х | |
| Просмотров: 3465 | Комментарии: 84 | |
| Всего комментариев: 84 | 1 2 3 » |
|
| |
| 1-15 16-30 31-42 | |